一些数学知识 |

以下内容是在学习中遇到的数学方面的知识，拾网上众人牙慧而整理出的（详见参考），随着不断遇到问题应该会不断更新。

new update:2022.3.29

矩阵/张量分解

SVD

Singular Value Decomposition，奇异值分解是广泛用于机器学习领域的算法，可以用于降维算法中的特征分解。当矩阵为方阵的时候，可以通过特征值和特征向量对矩阵进行分解：

\[A=W\sum W^T\]

其中，$W^TW=I$（酉矩阵），$\sum$为由特征值从小到大排列的主对角线矩阵。为了对非方阵矩阵也能进行分解，SVD被提出了。

\[A=U\sum V^T\]

其中，$A\in R^{m\times n},U\in R^{m \times m},\sum\in R^{m\times n},V\in R^{n\times n},U^TU=I,V^TV=I$，$\sum$除主对角线外其他元素均为0。

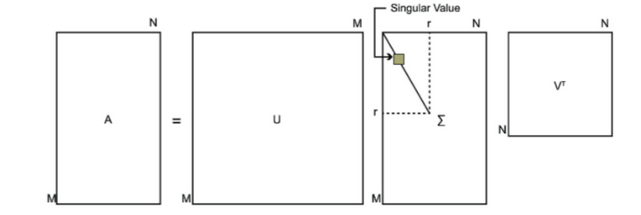
利用$A$的转置与它拼接出方阵以完成奇异值分解，通过$A^TA$得到一个$n\times n$的矩阵，对此进行特征分解：

\[(A^TA)v_i=\lambda_iv_i\]

将所有的$v$组成$V$，将$v$称为右奇异向量。通过$AA^T$得到一个$m\times m$的矩阵，对此进行特征分解：

\[(AA^T)u_i=\lambda_iu_i\]

将所有的$u$组成$U$，将$u$称为左奇异向量。

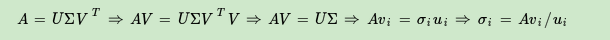
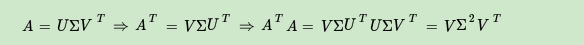
由此可以得出，奇异值矩阵的平方等于特征值矩阵（$AA^T$或$A^TT$）

NMF

非负矩阵分解（non-negative matrix factorization），于1999年由Lee和Seung发表于Nature。

对于任意一个给定的非负矩阵$V$，能找到一个非负矩阵$W$和一个非负矩阵$H$，满足$V=W*H$，将一个非负的矩阵分解为左右两个非负矩阵的乘积。$V$的每一列代表一个observation，每一行代表一个feature；$W$称为基矩阵，$H$为系数矩阵（或权重矩阵），用$H$代替$V$是一种降维过程。

\[V_{n\times m}=W_{n\times k}\cdot H_{k \times m}\]

$V$：数据矩阵，$\R^n$空间中的$m$个数据按列排序

$W$：基矩阵/词典/模式/主题，$\R^n$空间中的$k$个$n$维向量作为基向量按列排列

$H$：系数矩阵/回归因子/活化系数：列向量可以视为$V$经过$W$投影的坐标

迭代目标：$\min \Vert V-V^\prime \Vert^2=\sum_{ij}(V_{ij}-V_{ij}^\prime)^2$

迭代公式：

\[H_{ij}^{k+1}=H_{ij}^k\frac{({W^k}^T\cdot V)_{ij}}{({W^k}^T\cdot W^k\cdot H^k)_{ij}}\\ W_{ij}^{k+1}=W_{ij}^k\frac{(V\cdot{H^k}^T)_{ij}}{(W^k\cdot H^k\cdot{H^k}^T)_{ij}}\]

Canonical Decomposition（CP分解）

CP分解将张量分解为若干个张量的和，形式为以下的式子：

\[X\approx \sum_{r=1}^R a_r\otimes b_r \otimes c_r\\ X_{ijk}\approx \sum_{r=1}^R a_{ij}b_{jr}c_{kr}\]

其中，$\otimes$表示外积且每一组成项对应的张量秩为1。

将上述每一组向量集合记为因子矩阵，即$A=[a_1,a_2,\dots,a_R],B=[b_1,b_2,\dots,b_R],C=[c_1,c_2,\dots,c_R]$，于是CP分解可以写成以下矩阵形式：

\[X_{(1)}\approx A(C\odot B)^T\\ X_{(2)}\approx B(C\odot A)^T\\ X_{(3)}\approx C(B\odot A)^T\\\]

其中，$\odot$表示Khatri-Rao积，具体形式为$A\odot B=[a_1\otimes b_1, a_2 \otimes b_2, \dots, a_k\otimes b_k]$

拉普拉斯特征分解

拉普拉斯矩阵，又称导纳矩阵，基尔霍夫矩阵或离散拉普拉斯。给定具有$n$个顶点的简单图$G$，其拉普拉斯矩阵$L_{n\times n}$定义为：

\[L=D-A\]

其中$D$是度矩阵，$A$是图的邻接矩阵。在$L$中，如果$i=j$，则元素为该节点的度；如果$i\neq j$且节点$i$和节点$j$相邻，则元素值为1。其余为0。

$L$有以下性质：

$L$是对称的
$L$是半正定的
$L$是一个$M$矩阵（自身的逆矩阵为一个非负矩阵）
$L$的每一行和列总和为0（对于无向图）

对称归一化拉普拉斯矩阵定义为：

\[L^{sym}:=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\]

在$L^{sym}$中，如果$i=j$且度不为0，则元素为1；如果$i\neq j$且节点$i$和节点$j$相邻，则元素值为$-\frac{1}{\sqrt{deg(v_i)deg(v_j)}}$。其余为0。

随机游走归一化拉普拉斯矩阵定义为：

\[L^{rw}:=D^{-1}L=I-D^{-1}A\]

在$L^{rw}$中，如果$i=j$且度不为0，则元素为1；如果$i\neq j$且节点$i$和节点$j$相邻，则元素值为$-\frac{1}{deg(v_i)}$。其余为0。

Frobenius norm

F-范数，记为$\Vert \cdot\Vert_F$矩阵$A$的Frobenius范数定义为矩阵$A$各项元素的绝对值平方的总和开根:

\[\Vert X \Vert_F \overset{def}{=}\sqrt{\sum_{ij}X_{ij}^2}\]

KL divergence

KL散度，又叫相对熵和信息散度，是两个概率分布间差异的非对称性度量。

\[D_{KL}(p\Vert q)= \sum_{i=1}^N[p(x_i)\log p(x_i) - p(x_i)\log q(x_i)]\]

一般，$p(x_i)$为真实事件的概率分布，$q(x_i)$为拟合该事件的概率分布。

离散型随机变量的信息熵公式：

\[H(p)=H(X)=E_{x\sim p(x)}[-\log p(x)]=-\sum_{i=1}^np(x)\log p(x)\]

如果拟合事件概率分布和真实分布一样，相对熵等于0，否则大于0（KL散度是不对称的）

Bregman divergence

bregman divergence 简单点说就是一个抽象的对于距离的定义。对于欧式距离，可以写成：

\[d^2(x,y):=\sum_{i=1}^n(x_i-y_i)^2\\ <x,y>:=\sum_{i=1}^nx_iy_i\\ d^2(x,y)=\Vert x-y\Vert^2=<x-y,x-y>=\Vert x\Vert^2-\Vert y\Vert^2-<2y,x-y>\]

注意到$2y$是$\Vert y \Vert^2$的导数，因此$\Vert y\Vert^2+<2y,x-y>$的值便是函数$f(x)=\Vert x\Vert^2$在$y$点切线在$x$处的取值。

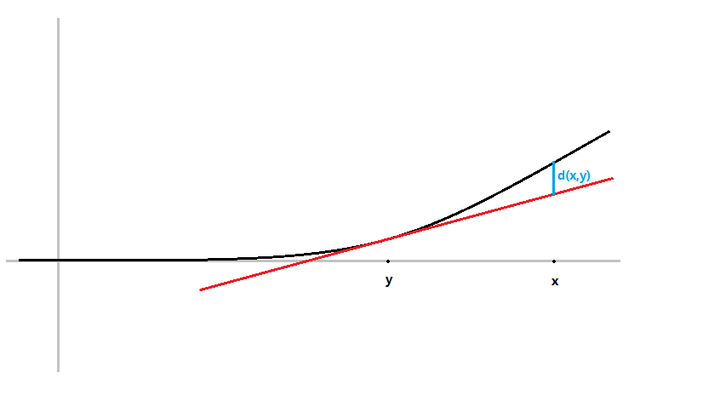
扩展这个定义，对距离进行定义：

\[d(x,y):=f(x)-(f(y)+<\triangledown f(y), x-y>)\\ f(x)\ge f(y)+<\triangledown f(y), x-y>,\forall x,y\in {\R}^n\]

Loss

Hinge Loss

铰链损失函数。针对于二分类问题，标签值为$y=\pm1$，预测值$\hat y\in \R$，需要一个这样的目标函数：当$\hat y > 1$和$\hat y < -1$时，分类器具有确定的结果，loss应当为0；当$\hat y\in (-1,1)$的时，分类器对于结果不确定，loss不为0。对于二分类问题可以做如下hinge loss定义：

\[l(y)=\max(0, 1-y\cdot\hat y)\]

Contrastive Loss

对比损失函数。用于孪生网络中的pair data之间比较。需要做到以下效果：1）近似样本之间的距离越小越好 2）不似样本之间的距离越大越好。

\[L=\frac{1}{2N}\sum_{n=1}^Nyd^2+(1-y)\max(margin-d,0)^2\]

$d$为欧式距离，$y=1$两样本匹配，$y=0$两样本不匹配。

Triplet Loss

用于训练差异性较小的样本。输入数据包括（Anchor，Postive和Negative），共享同样的模型设置

$L=[\Vert f(x_i^a)-f(x_i^p)\Vert^2_2-\Vert f(x_i^a)-f(x_i^n)\Vert^2_2+margin]_+$

公式

切比雪夫多项式

$T_n$和$U_n$都是区间[-1,1]上的正交多项式系。

第一类切比雪夫多项式

第一类切比雪夫多项式是以下微分方程的解：

\[(1-x^2)y^{\prime\prime}-xy^{\prime}+n^2y=0\]

形式为：

\[T_0(x)=1\\ T_1(x)=x\\ T_{n+1}(x)=2xT_n(x)-T_{n-1}(x)\]

此时母函数表示为：

\[\sum_{n=0}^\infty T_n(x)t^n=\frac{1-tx}{1-2tx+t^2}\]

第二类切比雪夫多项式

第二类切比雪夫多项式是以下微分方程的解：

\[(1-x^2)y^{\prime\prime}-3xy^{\prime}+n(n+2)y=0\]

形式为：

\[U_0(x)=1\\ U_1(x)=2x\\ U_{n+1}(x)=2xU_n(x)-U_{n-1}(x)\]

此时母函数表示为：

\[\sum_{n=0}^\infty U_n(x)t^n=\frac{1}{1-2tx+t^2}\]

FAC

Function-aware Componet，功能感知模块，出自论文《Task-orientedWord Embedding for Text Classification》。在FAC中，定义那些可以区分文本类别的词为关键词（salient word）。关键词会首先从训练集D中离线抽取，抽取的两条原则：

词$w$出现在第$k$类文档$D_k$的频率远高于在其他类别文档出现的频率
$w$在其他类别文档中的频率分布方差很小

衡量词$w$对于类别$k$关键性的评分函数：

\[Score(w,k)=\frac{t_k-\frac{1}{g}\sum_{1\le i \le g}t_i}{var(T_{-k}(w))}\]

$t_k$表示词$w$在第$k$类文档中的词频，$T_{-k}(w)$指词在非$k$类文档中的频率集合。

TPP

Temporal Point Processes（时间点过程），时间点过程可以对一系列历史事件建模，对未来进行预测。TPP使用条件概率函数$f(t\vert H_{t_n})$表示在给定历史$H_{t_n}$和时间$t_n<t\le T$的条件下的概率密度，累计密度函数（事件发生概率）写成：

\[F(t\vert H_{t_n})=\int_{\tau=t_n}^Tf(\tau\vert H_{t_n})d\tau\]

生存函数（survival function）表示了不发生的概率，也就是：$S(t\vert H_{t_n})=1-F(t\vert H_{t_n})$，下次事件发生的时间通过对于$f(\tau\vert H_{t_n})$的期望进行预测：

\[\hat t=\mathop{\mathbb E}_{t\sim f(t\vert H_{t_n})}[t]=\int_{\tau=t_n}^T \tau f(\tau\vert H_{t_n})d\tau\]

通过最大化整个过程的联合密度，可以对TPP的参数进行学习：

\[f(t_1,\dots,t_n)\prod_{i=1}^n f(t_i\vert H_{t_{i-1}})\]

另一种描述TPP的方法是使用条件强度函数，$\lambda(t\vert H_{t-})dt$表示在$t_n<t\leq T$区间都没有事件发生的情况下的时间间隔$[t,t+dt]$内发生事件的概率。$H_{t-1}$表示直到$t$之前的历史但不包括$t$，推导方式如下： $\begin{align*} \lambda(t\vert H_{t-})dt &= Prob(t_{n+1}\in[t,t+dt]\vert H_{t-})\\ &=Prob(t_{n+1}\in[t,t+dt]\vert H_{t_n},t_{n+1}\notin(t_n,t))\\ &=\frac{Prob(t_{n+1}\in[t,t+dt],t_{n+1}\notin(t_n,t)\vert H_{t_n})}{Prob(t_{n+1}\notin(t_n,t)\vert H_{t_n})}\\ &=\frac{Prob(t_{n+1}\in[t,t+dt]\vert H_{t_n})}{Prob(t_{n+1}\notin(t_n,t)\vert H_{t_n})}\\ &=\frac{f(t\vert H_{t_n})dt}{S(t\vert H_{t_n})} \end{align*}$

FT

傅里叶变换的目的是将时域（即时间域）上的信号转变为频域上的信号，随着域的不同，对同一个事物的了解角度也就随之改变，因此在时域中某些不好处理的部分，在频域就可以进行简单的处理。

傅里叶级数（Fourier series）最简单的理解方式就是任何周期函数都可以分解成一堆正弦函数，这里的正弦是$A\sin(wx+\varphi)$，又因为$\sin(\alpha+\beta)=\sin\alpha cos\beta+\cos\alpha \sin \beta$，可以把周期函数分解成一堆正弦与余弦函数。

傅里叶级数将$\{1,\sin x,\cos x,\sin 2x,\cos 2x,\cdots\}$看作空间中的基，展开为线性组合：$f(x)=\frac{a_0}{2}+\sum_{n=1}^{\infty}a_n\cos nx+b_n \sin nx$，其中：

\[a_0=\frac{1}{2\pi}\int_{-\pi}^{\pi}f(x)dx\\ a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\cos nxdx\\ b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)\sin nxdx\]

更一般的傅里叶级数公式：

\[f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty(a_n\cos\frac{2\pi nx}{T}+b_n\sin \frac{2\pi nx}{T})\\ a_n=\frac{2}{T}\int_{x_0}^{x_0+T}f(x)\cos \frac{2\pi nx}{T}dx\\ b_n=\frac{2}{T}\int_{x_0}^{x_0+T}f(x)\sin \frac{2\pi nx}{T}dx\]

利用欧拉公式：

\[e^{i\varphi}=\cos\varphi+i\sin\varphi\\ \cos\varphi=\frac{e^{i\varphi+e^{-i\varphi}}}{2}\\ \sin\varphi=\frac{e^{i\varphi-e^{-i\varphi}}}{2}\]

可以将傅里叶级数展开：

\[f(x)=\frac{a_0}{2}+\sum_{i=1}^\infty(a_n\frac{1}{2}(e^{i\frac{2n\pi x}{T}}+e^{-i\frac{2n\pi x}{T}})+b_n\frac{1}{2i}(e^{i\frac{2n\pi x}{T}}-e^{-i\frac{2n\pi x}{T}}))\\ =\sum_{-\infty}^\infty c_ne^{i\frac{2n\pi x}{T}}\\ c_n=\frac{1}{T}\int_{x_0}^{x_o+T}f(x)e^{-i\frac{2n\pi x}{T}}dx\\ w_0=\frac{2\pi}{T}\]

将非周期函数的周期看成无穷大，当$T\to\infty$时，$w_0\to0$，令$w=nw_0,F(w)=\frac{1}{T}\int_{-\infty}^\infty f(x)e^{-iwx}dx$，去掉$\frac{1}{T}$，有：

\[F(w)=\int_{-\infty}^\infty f(x)e^{-iwx}dx\\ f(x)=\frac{1}{2\pi}\int_{-\infty}^\infty F(w)e^{iwx}dw\]

PMI

PMI是一种用来衡量两个事物之间相似性的指标：

\[PMI(x,y)=lb\frac{p(xy)}{p(x)p(y)}\]

reparameterization trick

假设需要对如下期望，求关于$\theta$的梯度：

$\mathbb E_{p(z)}[f_\theta(z)]$ 其中，$p$是概率密度函数（与$\theta$无关）。如果函数$f_\theta(z)$本身关于$\theta$梯度存在，则：

$\begin{align} \nabla_\theta \mathbb{E}_{p(z)} [f_\theta(z)]& = \nabla_\theta[\int_{z}p(z)f_\theta(z)dz]\\ &= \int_z p(z) [\nabla_\theta f_\theta(z)] dz \\ &= \mathbb{E}_{p(z)} [\nabla_\theta f_\theta(z)] \end{align}\\$

从上面可以看出，期望的梯度等于梯度的期望。

如果密度函数$p$也有参数$\theta$呢，即$p\to p_\theta$，重复上述步骤：

$\begin{align} \nabla_\theta \mathbb{E}_{p_\theta(z)} [f_\theta(z)]& = \nabla_\theta[\int_{z}p_\theta (z) f_\theta(z)dz]\\ &= \int_z \nabla_\theta [p_\theta(z) f_\theta(z)] dz \\ &= \int_z f_\theta(z) \nabla_\theta p_\theta(z) dz + \int_z p_\theta(z) \nabla_\theta f_\theta(z) dz \\ &=\underbrace{\int_z f_\theta(z) \nabla_\theta p_\theta (z)dz}_{\text{What about this?}}+ \mathbb{E}_{p_\theta (z)} [\nabla_\theta f_\theta(z)] \end{align}\\$

最终得到的式子中，第一项不属于任何函数的期望，简单来说就是无法将$\bigtriangledown_\theta p_\theta(z)$写出来，使用重参数化技巧来解决这个问题。

$\begin{align} \bm{\epsilon} & \sim p(\bm{\epsilon}) \tag{R1}\\ \bm{z} & = g_\theta(\bm{\epsilon}, \bm{x}) \tag{R2}\\ \Rightarrow \mathbb{E}_{p_\theta(z)} [f(\bm{z}^{(i)})] & = \mathbb{E}_{p(\epsilon)} [f( g_\theta(\bm{\epsilon}, \bm{x}^{(i)}) )] \tag{R3}\\ \Rightarrow \nabla_\theta \mathbb{E}_{p_\theta(z)} [f(\bm{z}^{(i)})] & = \nabla_\theta \mathbb{E}_{p(\epsilon)} [f( g_\theta(\bm{\epsilon}, \bm{x}^{(i)}) )] \tag{a}\\ & = \mathbb{E}_{p(\epsilon)} [\nabla_\theta f( g_\theta(\bm{\epsilon}, \bm{x}^{(i)}) )] \tag{b} \\ & \approx \dfrac{1}{L} \sum_{l=1}^{L}{\nabla_\theta f( g_\theta(\bm{\epsilon}^{(l)}, \bm{x}^{(i)}) )} \tag{c} \end{align}\\$

其中，R1和R2是重参数化技巧的通用步骤：将随机变量$z$中的随机性与数据正式信息解耦。R3的话是将R2代入原先无法求梯度的期望后的结果，核心点在于期望对象的变化。那么，通过a/b/c步运算以后，我们可以将期望的梯度，转换成梯度的期望，并使用Monte Carlo方法进行近似求解。

VAE中的情形

在VAE中，ELBO（evidence lower-bound）写作：

$ELBO(\theta, \phi) = \underbrace{\mathbb{E}_{q_\phi(z)} [log p_\theta(\bm{x,z}) - log q_\phi (\bm{z|x}) ]}_{\mathcal{L}} \tag{2}$

区分了模型参数$\theta$和隐变量$\phi$，那么梯度表示为：

$\nabla_{\theta, \phi}ELBO(\theta, \phi) = \nabla_{\theta, \phi}[\mathbb{E}_{q_\phi(z)} [log p_\theta(\bm{x,z}) - log q_\phi (\bm{z|x}) ] ] \\$

假设先验和厚颜估计均为高斯分布的时候，上面的式子可以进一步简化为：

$\nabla_{\theta, \phi} \mathcal{L}=- \nabla_{\theta, \phi} \underbrace{[KL[q_\phi( \bm{z}| \bm{x}^{(i)}) || p_\theta( \bm{z})]]}_{\text{Analytically compute this}} + \nabla_{\theta, \phi} \overbrace{\dfrac{1}{L} \sum_{l=1}^L (log p_\theta( \bm{x}^{(i)} | \bm{z}^{(l)}))}^{\text{Monte Carlo estimation}}\\$

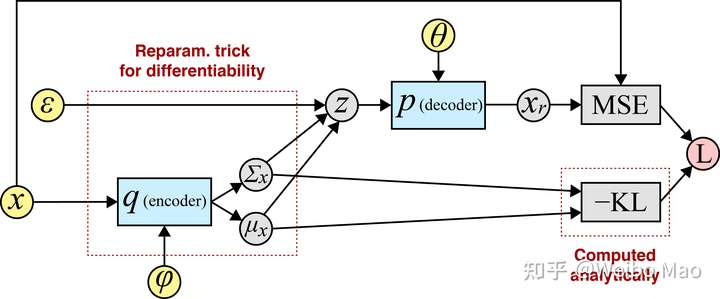
从encoder-decoder角度看ELBO的话：

$\mathcal{L}=- KL[\underbrace{q_\phi( \bm{z}| \bm{x}^{(i)}) }_{\text{Encoder}} || \underbrace{p_\theta( \bm{z})}_{\text{Fixed}}] + \dfrac{1}{L} \sum_{l=1}^L log \overbrace{p_\theta( \bm{x}^{(i)} | \bm{z}^{(l)})}^{\text{Decoder}}\\$

其中，将 $q_\phi( \bm{z}| \bm{x}^{(i)}) = \mathcal{N}(\mu_x, \sigma_x)$ ， $p_\theta( \bm{z}) = \mathcal{N}(0, I)$ 后，即可得到代码中常用的KL loss项的表达公式：

分布

以下内容参考《LDA数学八卦》中整理出，考虑到“实用主义”，没有认真把每一步推导都过一遍，把主要结论和用法摘录出来了。

Gamma分布

Gamma函数为：

\[\Gamma(x)=\int_0^\infty t^{x-1}e^{-t}dt\]

Gamma函数有一个重要的性质：$\Gamma(x+1)=x\Gamma(x)$，且$\Gamma(n)=(n-1)!$，Gamma函数产生的意义是将阶乘推广到了实数领域。

对Gamma函数进行变形可以下面的式子：

\[\int_0^\infty \frac{x^{\alpha-1}e^{-x}}{\Gamma(\alpha)}dx=1\]

取积分中的函数作为概率密度，就得到一个Gamma分布的密度函数：

\[Gamma(x\vert \alpha)=\frac{x^{\alpha-1}e^{-x}}{\Gamma(\alpha)}\]

令$x=\beta t$，得到一般的Gamma分布的密度函数：

\[Gamma(t\vert \alpha,\beta)=\frac{\beta^\alpha t^{\alpha-1}e^{-\beta t}}{\Gamma(\alpha)}\]

在gamma相关的函数中有一个重要函数，称作Digamma函数：

\[\Psi(x)=\frac{d\log \Gamma(x)}{dx}\]

其具有一个漂亮的性质：

\[\Psi(x+1)=\Psi(x)+\frac{1}{x}\]

Beta分布

假设一个问题，问题1：从0-1中随机生成$n$个数，其中第$k$大的数分布情况是怎样？

结论是：

\[f(x)=\frac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)}x^{\alpha-1}(1-x)^{\beta-1},\\ \alpha=k,\beta=n-k+1\]

由此可以得到了基于Beta分布的先验分布，也就是说在没有进行采样之前，认为问题1中的结果分布服从Beta分布。

如果进行取样，得到一个新问题，问题2：在问题1的基础上，给出一系列采样结果，假设$p$是第$k$个数字，采样中$m_1$个数比$p$小，$m_2$个数比$p$大，此时$p$的分布是怎样？

一个直观的类比为先验知识告诉我们在抛硬币的时候，正面朝上的概率为0.5，这就是先验分布的结果，假如这是个质地不均匀的硬币，那么显然从统计上来说，最终正面朝上的概率不是0.5，这就是贝叶斯参数估计的过程：先验分布+数据的知识=后验分布。

将问题2抽象为数学表达：

先验分布：$Beta(p\vert k, n-k+1)$

数据的知识：$BinomCount(m_1,m_2)$，此处$m_1$服从二项分布$B(m,p)$，因为$m_1+m_2=m$，本质上就是做了$m$次伯努利试验。

最终的结果就是：$Beta(p\vert k, n-k+1)+BinomCount(m_1,m_2)=Beta(p\vert k+m_1,n-k+1+m_2)$

一般形式的表示：

\[Beta(p\vert \alpha, \beta)+BinomCount(m_1,m_2)=Beta(p\vert \alpha+m_1,\beta+m_2)\]

上式描述的就是Beta-Binomial共轭，这个式子也可以转换为另一种形式：

\[Beta(p\vert 1, 1)+BinomCount(\alpha-1,\beta-1)=Beta(p\vert \alpha,\beta)\]

注意$Beta(p\vert1,1)=Uniform(0,1)$。

关于期望，有$E(p)=\frac{\alpha}{\alpha+\beta}$。

Dirichlet分布

Dirichlet分布也是在人工智能领域经常出现的一个模型，用来解决以下问题，问题3：给定$n$个0-1之间的随机数，求此时其中第$k_1,k_2,\dots,k_l$大数字的联合分布。

直观上就是将Beta分布推广到多维的情形，对于问题3，将每个变量记为向量的形式：$\vec{p}=(p_1,p_2,\dots,p_l)$，给定一个限制：$p_l=1-(p_1+p_2+\cdots+p_{l-1})$将参数同样也记为向量的形式：$\vec{k}=(k_1,k_2,\dots,k_l)$，得到先验分布：$Dir(\vec{p}\vert\vec{k})$。与Beta分布中的问题2类似，此时进行取样，落在各个区间的个数也记为向量的形式：$\vec{m}={m_1,m_2,\dots,m_l}$，此时就有：

\[Dir(\vec{p}\vert\vec{k})+MultiCount(\vec{m})=Dir(\vec{p}\vert \vec{k}+\vec{m})\]

令$\vec{\alpha}=\vec{k}$，从整数集合延拓到实数集合，更一般的形式为：

\[Dir(\vec{p}\vert\vec{\alpha})+MultiCount(\vec{m})=Dir(\vec{p}\vert \vec{\alpha}+\vec{m})\]

上式就是Dirichlet-MultiCount共轭，同样，这个式子也可以转换为另一种形式：

\[Dir(\vec{p}\vert\vec{1})+MultiCount(\vec{m}-\vec{1})=Dir(\vec{p}\vert \vec{\alpha})\]

一般形式的Dirichlet分布定义如下：

\[Dir(\vec{p}\vert \vec{\alpha})=\frac{\Gamma(\sum_{k=1}^K \alpha_k)}{\prod_{k=1}^K\Gamma(\alpha_k)}\prod_{k=1}^K p_k^{a_{k}-1}\]

对于给定的$\vec{p}$和$N$，多项分布定义为：

\[Mult(\vec{n}\vert \vec{p},N)=\binom{N}{\vec{n}}\prod_{k=1}^Kp_k^{n_k}\]

关于期望，有:

\[E(\vec{p})=(\frac{\alpha_1}{\sum_{i=1}^K\alpha_i},\frac{\alpha_2}{\sum_{i=1}^K\alpha_i},\cdots,\frac{\alpha_K}{\sum_{i=1}^K\alpha_i},)\]

Dirichlet极大似然估计

Dirichlet最常用的地方是作为多项分布的先验分布。多项分布和Dirichlet分布形成一个共轭先验对，有下列式子成立：

\[p(x\vert \theta)p(\theta)=Mult(x\vert \theta)Dir(\theta\vert \alpha)=Dir(x+\alpha)\]

给定一组观测到的多项数据，$D=\{\rm p_1,p_2,\dots,p_N\}$，可以通过极大log似然函数来估计Dirichlet分布：

\[F(\alpha)=\log p(D\vert \alpha) = \log \prod_i p({\rm p}_i\vert \alpha)\\ = log\prod_i \frac{\Gamma(\sum_k \alpha_k)}{\prod_k \Gamma(\alpha_k)}\prod_k p_{ik}^{\alpha_k-1}\\ =N(\log \Gamma(\sum_k a_k)-\sum_k \log \Gamma(\alpha_k)+\sum_k(a_k-1)\log \hat{p}_k)\\ \log \hat{p}_k =\frac{1}{N}\sum_i \log p_{ik}\]

如果使用梯度下降法：

\[\frac{dF}{d a_k}=N(\Psi(\sum_k \alpha_k)-\Psi(\alpha_k)+\log \hat{p}_k)\]

参考

奇异值分解（SVD） - 知乎 (zhihu.com)

图卷积神经网络(GCN)详解:包括了数学基础(傅里叶，拉普拉斯) - 知乎 (zhihu.com)

切比雪夫多项式 - 简书 (jianshu.com)

VAE中的重参数化技巧-reparameterization trick - 知乎 (zhihu.com)

《LDA数学八卦》–靳志辉

《Maximum Likelihood Estimation of Dirichlet Distribution Parameters》

『矩阵论笔记』张量CP分解的详细数学推导以及Python实现_布衣小张的博客-CSDN博客

- 剑杪 -

目录

一些数学知识

矩阵/张量分解

SVD