根据阅读进度，时不时会更新

[toc]

TDGNN

Continuous-Time Link Prediction via Temporal Dependent Graph Neural Network,2020

在传统的GNN中，邻接节点的权重都是一致的，TDGNN使用幂函数对邻接节点使用不同的权重，对于与目标节点关联更近的节点有更大的权重。

给定一个静态的无向图\(G=(V,E)\)，使用GCN可以得到节点\(v_i\)的第\(l\)层的向量表示\(\vec{h}_v^l\)：

\[\vec{h}_v^l=\sigma(W_l\sum_{u\in N(v)\cup v}\frac{\vec{h}_v^{l-1}}{\sqrt{\vert N(u)\vert \vert N(v)\vert}})\]

可以看到GCN对于每个邻居节点的权重都是一致的，这样做无视了图谱中边的信息，尤其对于包含了时序信息的动态图谱。

TDGNN的输入是一个有着边时序信息的动态图谱\(G=(V,E^T,T,X)\)，其中\(X=\{\vec{x}_1,\vec{x}_2,\cdots,\vec{x}_n\},\vec{x}_i \in R^P\)是节点特征。TDGNN的输出是一组在时刻\(t\)的新的节点表示\(H=\{\vec{h}^t_1,\vec{h}^t_2,\cdots, \vec{h}^t_n \},\vec{h}^t_i\in R^d\)和边表示\(S=\{\vec{s}_1^t,\vec{s}_2^t,\cdots,\vec{s}_q^t \},\vec{s}_j^t\in R^m\)。在时刻0的时候有\(\vec{h}_0^v=\vec{x}_v\)，时刻\(t\)可以通过以下公式计算（TDAgg）：

\[\vec{h}_v^k=\sigma(\sum_{u\in N_t(v)\cup v}\alpha^{t}_{vu}W\vec{h}_u^{k-1})\\ \alpha_{vu}^t=\frac{e^{t-t_{v,u}}}{\sum_{u\in N_t(v)\cup v}e^{t-t_{v,u}}}\]

也就是如果一条边越早被建立，那么将它聚合到节点时所占的比重会越大。

RE-NET

Recurrent Event Network: Autoregressive Structure Inference over Temporal Knowledge Graphs,EMNLP2020

时间聚合

s:subject, r:relation, o:object \(s\to r \to o\)

关于节点聚合的几种方法

Mean Pooling Aggregator

形式为\(\{e_o:o\in N_t^{(s,t)} \}\)，其中\(N_t^{(s,r)}\)是在时间\(t\)时以\(s\)为开始的关系为\(r\)的所有\(o\)。平均聚合没有考虑不同的邻居的权重。

Attentive Pooling Aggregator

形式为\(g(N_t^{(s,t)})=\sum_{o\in N_t^{(s,t)}}\alpha_oe_o\)，其中\(\alpha_o=softmax({\rm v^T}\tanh(W(e_s;e_r;e_o)))\)。其中\(v\in R^d,W\in R^{d\times 3d}\)是可训练参数权重矩阵，权重可以决定每个尾实体对于头实体和关系的关联程度。

Multi-Relational Graph (RGCN) Aggregator

将多关系和多跳邻居信息进行聚合，形式为:

\[g(N_t^{(s)})=h_s^{(l+1)}=\sigma(\sum_{r\in R}\sum_{o\in N_t^{(s,r)}}\frac{1}{c_s}W_r^{(l)}h_o^{(l)}+W_0^{(t)}h_s^{(l)})\]

初始的每个节点\(h_o^{(0)}\)的隐藏向量表示为\(e_o\)，对于每个节点使用\(c_s\)进行归一化。每个关系都可以在实体之间派生出一个局部图结构，通过聚合邻居信息可以进一步产生消息（message），例如：\(\sum_{o\in N_t^{(s,r)}}\frac{1}{c_s}W_r^{(l)}h_o^{(l)}\)。通过聚合所有特定关系的消息，进一步计算每个实体上的总体消息，例如\(\sum_{r\in R}\sum_{o\in N_t^{(s,r)}}\frac{1}{c_s}W_r^{(l)}h_o^{(l)}\)。最终，对于\(g(N_t^{(s)})\)的的定义包含了所有的消息和之前步骤的信息（\(W_0^{(t)}h_s^{(l)}\)）。

为了区分不同的关系之间的权重，论文对每个关系\(r\)采取了独立的权重矩阵\(W_r^{(l)}\)，聚合器通过引入神经网络的多层，每层用\(l\)索引来收集多跳邻居的表示，层数决定了节点从其局部邻域聚合信息所到达的深度。这个聚合器的主要问题是随着关系数量的提升，参数数量也会极速提升，在实际应用中，这样会导致对于稀少关系的漂移。因此，论文采用了block-diagonal分解，每个特定关系的权重矩阵通过降维分解为了block-diagonal。\(W_r^{(l)}\)被定义为区块对角矩阵，\(diag(A_{1r}^{(l)},\dots,A_{Br}^{(l)}),A_{kr}^{(l)}\in R^{(d(l+1)/B)\times(d^{l}/B)}\)，\(B\)是基础矩阵的个数。

Recurrent Event Network

定义所有事件的联合分布为\(G=\{G_1,\dots,G_T \}\)。联合分布可以写成下面的形式：

RE-NET同时使用全局和局部表示。全局表示\(H_t\)总结了直到时间戳\(t\)的所有整个图谱的全局信息，反应了在即将到来的时间下的全局偏向性。局部表示聚焦于每个subject实体\(s\)和每对subject实体和关系\((s,r)\)，分别定义为\(h_t(s)\)和\(h_t(s,r)\)。

RE-NET的参数可以认为是下面的形式：

\[p(o_t\vert s,r,G_{t-m:t-1})\propto \exp([e_s:e_r:h_{t-1}(s,r)]^T\cdot w_{o_t})\\ e_s,e_r,h_{t-1}(s,r)\in R^d\]

将MLP解码器定义为一个由\(w_{o_t}\)参数化的线性软最大分类器。类似的，可以定义relation和subject：

\[p(r_t\vert s, G_{t-m:t-1})\propto \exp([e_s:h_{t-1}(s)]^T\cdot w_{r_t}) \\ p(s_t\vert G_{t-m:t-1})\propto \exp(H^T_{t-1}\cdot w_{s_t})\]

使用下列形式定义全局和局部表示：

\[H_t ={\rm RNN^1}(g(G_t),H_{t-1}),\\ h_t(s,t)={\rm RNN}^2(g(N_t^{(s)},H_t,h_{t-1}(s,r))),\\ h_t(s)={\rm RNN}^3(g(N_t^{(s)}),H_t,h_{t-1}(s))\]

对于连接预测任务可以认为是一个多分类的任务，损失函数可以定义为：

\[\mathcal L=-\sum_{(s,r,o,t)\in G}\log p(o_t\vert s_t,r_t)+\lambda_1\log p(r_t\vert s_t)+\lambda_2 \log p(s_t)\]

\(\lambda_1\)和\(\lambda_2\)是超参数，如果任务是给定\((s,r)\)预测\(o\)，那么可以给定较小的\(\lambda_1\)和\(\lambda_2\)。

基于时间的多步推理：

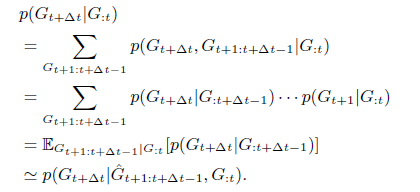
算法流程图如下：

TeMP

TeMP: Temporal Message Passing for Temporal Knowledge Graph Completion,EMNLP2020

消息传递+时序聚合

论文将编码器分为了结构实体表示（structed entity，简称SE）和时序表示（temporal，简称TE），SE基于多关系消息传递网络去表示实体：\(x_{i,t}=SE(e_i,D^{(t)})\)，TE聚合在当前时间\(t\)前的SE的输出结果，即达到聚合时间信息的目的：\(z_{i,t}=TE(x_{i,t-\tau},\dots,x_{i,t})\)。

SE

SE使用了常见的基于关系的消息传递机制（R-GCN）： \(h_{i,t}^{(0)}=W_0u_i,\forall t\in0,\dots,T,\\ h_{i,t}^{(l+1)}=\sigma(\sum_{r\in R} \sum_{j\in N_i^\tau} \frac{1}{\vert N_i^T \vert} W_r^{(l)}h_{j,k}^{(l)}+W_s^{(l)}h_{i,t}^{(l)})\\ x_{i,t}=h_{i,t}^{(L)}\)

TE

论文使用两种方法来对时间建模实体表示\(z_{i,t}\)，第一个是结合传统递归机制和权重衰减机制的模型（TeMP-GRU）来模拟历史事件对当前时间点事件的影响随时间发展而逐渐消退的情形。设定\(t^-\)表示在时间\(t\)之前\(e_i\)最后一次激活的时间，使用以下式子： \(\hat{z}_{i,t^-}=\gamma^z_{i,t^-}z_{i,t^-}\\ \gamma^z_{i,t^-}=\exp\{-\max(0,\lambda_z \vert t-t^-\vert+b_z\}\\ z_{i,t}=GRU(x_{i,t},\hat{z}_{i,t^-})\)

第二个是使用了自注意力机制的模型（TeMP-SA），公式如下： \(q_{ij}=\frac{(x_{i,t}W_q)(x_{i,t-j}W_k)^T}{\sqrt{d}}\\ e_{ij}=q_{ij}-\max(0,\lambda_zj+b_z)+M_{ij}\\ \beta_{ij}=\frac{\exp(e_{ij})}{\sum_{k=0}^\tau \exp(e_{ik})}\\ z_{i,t}=\sum_{j=0}^\tau \beta_{ij}(x_{i,t-j}W_v)\)

使用\(M\)作为mask矩阵，当在时间\(t-j\)时如果\(e_i\)被激活，使得值为0，否则为\(-\infin\)。

时间异构

时序知识图谱中的异构主要体现在实体出现的稀疏性和多样性。在对每个快照训练时，会忽视此时刻没被激活的实体。使用一种归属（imputation，IM）方法来将非活跃实体与时间结合，也就是在原R-GCN的方法上加入了与时间交互，使得如果在最近激活过的实体但在该时刻未激活过的实体更偏向之前的实体表示： \(\gamma^x_{i,t^-}=\exp\{-\max(0,\lambda_x \vert t-t^-\vert+b_x\}\\ \hat{x}_{i,t}=\gamma_{i,t^-}^xx_{i,t^-}+(1-\gamma_{i,t^-}^x)x_{i,t}\)

此外还使用一种基于频率的门机制（frequency-based gating，FG）对实体的结构编码和时序编码进行融合。首先定义频率，subject实体频率\(f_s^t\)，object实体频率\(f_o^t\)，relation频率\(f_r^t\)，sub-rel频率\(f_{s,r}^t\)，rel-obj频率\(f_{r,o}^t\)，\(F_s=[f_s^t,f_r^t,f_{s,r}^t]\)，于是定义新的实体表示如下： \(\tilde{z}_{s,t}=\alpha_{os}x_{s,t}+(1-\alpha_{os})z_{s,t}\\ \tilde{z}_{o,t}=\alpha_{oo}x_{o,t}+(1-\alpha_{oo})z_{o,t}\\ \alpha_{os}=MLP_{os}(F_s),\alpha_{oo}=MLP_{oo}(F_s)\)

解码器

论文中的解码器采用的是TransE的解码器。

ATiSE

Temporal Knowledge Graph Completion Based on Time Series Gaussian Embedding, ISWC2020

距离模型+时间建模

论文使用了一种叠加的时间序列嵌入模型。对于一个时间序列分为三个部分构成： \(Y_t=T_t+S_t+R_t\)

其中，\(T_t\)为趋势模块（trend），\(S_t\)为周期模块（seasonal），\(R_t\)为噪声模块。独立于时间的实体和关系表示分别为\(e_i\)和\(r_p\)，并有\(\Vert e_i\Vert_2=1,\Vert r_p \Vert_2=1\),在此基础上增加前面所述的时间模块： \(e_{i,t}=e_i+\alpha_{e,i}w_{e,i}t+\beta_{e,i}\sin(2\pi w_{e,i}t)+{\mathcal N}(0,\Sigma_{e,i})\\ r_{p,t}=r_p+\alpha_{r,p}w_{r,p}t+\beta_{r,p}\sin(2\pi w_{r,p}t)+{\mathcal N}(0,\Sigma_{r,p})\\\)

其中，\(\Vert w_{e,i}\Vert_2=1,\Vert w_{r,p} \Vert_2=1\)。

对于一个四元组\((s,p,o,t)\)，基于距离的KGE模型有\(P_{e,t}= P_{s,t}-P_{o,t}\)，使用概率分布的形式表示为\(P_{e,t}\sim {\mathcal N}(\mu_{e,t},\Sigma_e)\)，其中\(\mu_{e,t}=\overline{e}_{s,t}-\overline{e}_{o,t},\Sigma_e=\Sigma_s+\Sigma_o\)，与关系r原本的分布\(P_{r,t}\sim {\mathcal N}(r_{p,t},\Sigma_r)\)进行对比，论文使用KL散度来计算两个分布的离散程度，因为KL散度的计算前后顺序会有不同的结果，所以论文中采用加权取平均： \(f_t(e_s,r_p,e_o)=\frac{1}{2}({\mathcal D_{\mathcal K \mathcal L}}(P_{r,t},P_{e,t})+ {\mathcal D_{\mathcal K \mathcal L}}(P_{e,t},P_{r,t}))\)

TeRo

TeRo: A Time-aware Knowledge Graph Embedding via Temporal Rotation, COLING2020

距离模型+时序旋转

论文将实体嵌入在复数向量空间的旋转视为在时间上的变化，也就有\(s,r,o\in \mathbb C^k\)，转换方程定义为： \(s_t=s\circ \tau, o_t=o\circ \tau,\tau\in \mathbb C^k\)

其中，\(\circ\)表示复数向量之间的哈密尔顿点乘，定义\(\vert\tau_j \vert=1\)，这样就可以用\(e^{i\theta_{\tau,j}}\)的形式表示\(\tau_j\)。对于评分函数定义为： \(f_{TeRo}(s,r,o,t)=\Vert s_t+r-\overline{o}_t\Vert\)

对于持续一段时间的事件，开始时间记为\(t_b\)，结束时间记为\(t_e\)，有： \(f_{TeRo}(s,r,o,[t_b,t_e])=\frac{1}{2}( \Vert s_{t_b}+r_b-\overline{o}_{t_b}\Vert+\Vert s_{t_e}+r_e-\overline{o}_{t_e}\Vert)\)

论文定义了三种不同的关系模式：

1. 时序关系（temporary）：\(if\ \exists o,t_1,t_2\ r(s,o,t_1) \and \neg r(s,o,t_2)\)，即同一个关系在不同时间不一定成立。
2. 非对称关系（asymmetric）： \(if \ \exist s,o,t, r(s,o,t)\and \neg r(o,s,t)\)，即不对称的关系
3. 自反关系（reflexive）：\(if\ \exist s,t\ r(s,s,t)\)

基于以上定义可以对关系进行限制，现有事实\((s,r,o,t_1),s_{t_1}+r=\overline{o}_{t_1}\)：

1. 对于时序关系，令\(s_{t_2}+r\ne \overline{o}_{t_2}\)
2. 对于非对称关系，令\(\overline{o}_{t_2}+r\ne s_{t_2}\)
3. 对于自反关系，令\(Im(r)=2Im(s_{t_1})\)，可以将多个自反关系表示为不同的嵌入

T-SimplE

Tensor Decomposition-Based Temporal Knowledge Graph Embedding, ICTAI 2020

张量分解

论文基于CP分解（关于CP分解可看此），CP分解将一个高维的张量表示为秩为1的向量和： \(X\approx \sum_{d=1}^D h_d\circ r_d \circ t_d\\ h_d\in \mathbb R^I, r_d\in \mathbb R^J,t_d\in \mathbb R^K\)

写成矩阵形式： \(X_{(1)}\approx H(R\odot T)^\mathrm T\\ X_{(2)}\approx R(H\odot T)^\mathrm T\\ X_{(3)}\approx T(R\odot H)^\mathrm T\)

在静态图中只需要三个维度就够了，在TKG中，论文增加了一个时间维度来对基于张量分解的方法进行扩展。

T-ComplEx拓展了T-DistMult方法，使用复数来表示实体和关系。\(re_e\in \mathbb R^d\)和\(im_e\in \mathbb R^d\)分别表示实体\(e\)的实部和虚部，\(re_r\in \mathbb R^d\)和\(im_r\in \mathbb R^d\)分别表示关系\(r\)的实部和虚部，在此基础上，为拓展时空关系，增加了一个新的因子\(w_\tau\in \mathbb R^d\)，换句话说就是在虚数空间的基础上又增加了一个新的维度，对于一个四元组\((e_i,r,e_j,\tau)\)的相似度方程定义如下： \(<re_{e_i},re_r,re_{e_j},w_\tau>+<re_{e_i},im_r,im_{e_j},w_\tau>+<im_{e_i},re_r,im_{e_j},w_\tau>-<im_{e_i},im_r,re_{e_j},w_\tau>\)

论文中未采用虚数空间，而是对每个实体\(e\)赋予两个向量\(h_e,t_e\in \mathbb R^d\)分别表示头实体和尾实体，关系\(r\)也有两个向量\(v_r,v_{r-1}\in \mathbb R^d\)，同样增加要给新的因子\(w_\tau\in \mathbb R^d\)，此时相似度方程定义为： \(\frac{1}{2}(<h_{e_i},v_r,t_{e_j},w_\tau>+<h_{e_j},v_{r^{-1}},t_{e_i},w_\tau>)\)

有些特征对时间敏感，有些不敏感，设置一个参数\(\alpha \in [1,d]\)来控制敏感程度，越不敏感，对应的向量为1越多： \(\frac{1}{2}(<h_{e_i},v_r,t_{e_j},[w_{\tau\alpha}:1]>+<h_{e_j},v_{r^{-1}},t_{e_i},[w_{\tau\alpha}:1]>)\)

对于时间结合的方法可以用哈密尔顿乘法，例如： \(<h_{e_i},v_r,t_{e_j}\odot[w_{\tau\alpha}:1]>\)

训练中设置两个训练目标：\((h,r,?,\tau)\)和\((?,r,t,\tau)\)，训练方法采用正负采样方法。