ML常见模型汇总

写在前面

在神经网络中，有很多复杂的模型，个人感觉很多基本的模型就像是乐高中的零件，总能用它们或者它们的变体组合出很多新鲜的玩意，搞懂这些论文中经常提及的基本模型，是研究机器学习的一个必经之步，这篇文章就是用来记录我学习的过程和对各类模型的总结（会不定时一直更新）。

update:2020.9.23 RNN、LSTM

RNN（循环神经网络）

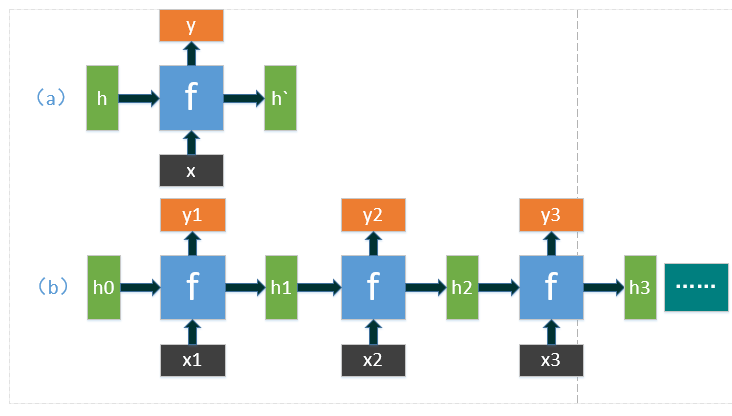
上图为RNN的基本结构图，图（a）中为RNN的缩略结构，可以看到\(x\)为当前输入，\(h\)为上一步的状态输出，此时为当前的另一个输入，\(y\)为当前结果的输出，\(h'\)为当前状态的输出，将\(f\)定义为关于\(h\)和\(x\)的函数：\(h',y=f(h,x)\),之所以这种网络被称为循环神经网络，就是因为无论输入输出的序列有多长，始终用到的函数只有\(f\)，图（b）就展现了这种特性。

在应用中，结果\(y\)通常是由\(h'\)通过一个线性层然后使用softmax等进行分类得到，具体模型会应用不同的方法。

LSTMs（长短期记忆网络）

传统的RNN会有梯度爆炸的问题（因为反向传播中链式法则的存在，对于深层网络容易有梯度越算越小最终消失的情况）和长期依赖的问题。于是有了LSTMs，它能够在更长的序列中有更好的表现。

RNN通过一个参数\(h^t\)来进行状态的传递，而LSTM有两个参数来传递状态，一个参数是\(c^t\)（cell state），一个是\(h^t\)（hidden state），简要的说，\(c^t\)的传递改变很慢，\(h^t\)相对来说改变的较快快。

LSTM中最核心的部分就是cell state（下图中的\(c^{t}\)），它的传递方式很像传送带，在整个网络中一路向下的传递，中间只产生一些小的线性交互，这使得cell state很容易可以保持不变（起到长期存储的目的）。为了能在cell state中增加或删除某些信息，LSTM使用了一些门结构。

LSTM中有三个作为门控状态的值\(z^f,z^i,z^o\)，分别对应forget，input和output这些值都是在0到1之间（为了决定每个元素的保留的程度），通过以下式子得到这些值： \(z^k=\sigma(w^k\cdot v),k\in(f,i,o)\) 其中，\(w^t\)为权重矩阵，\(v\)为当前输入\(x^t\)与上个状态传递的\(h^{t-1}\)拼接而成得到的一个向量，\(\sigma\)为sigmoid激活函数。除此之外，还有一个参数\(z\)，计算公式为：\(z=tanh(w\cdot v)\)。LSTM的作用机理一般分为三步（参考下图）：

1. LSTM决定哪些信息应该从cell state中丢弃，这一层网络被称为为遗忘门，通过\(z^f\)与\(c^{t-1}\)对应元素逐项相乘得到结果（如果\(z^f\)中某一元素为0，意味着完全丢弃\(c^{t-1}\)中的对应元素）。
2. LSTM决定哪些信息需要增加到cell state中去。一个输入门\(z^i\)决定哪些值需要得到更新，同时，\(z\)为需要被增加到cell state的值，将这两者结合的结果加到cell state中去。到这里，cell state就更新完成了，简而言之就是对cell state先进行遗忘再进行记忆，以到达重要信息不管多久远都可以被记录，不重要信息在传递中会被丢弃掉的目的。
3. LSTM决定哪些值需要被输出。这里需要对更新完成的cell state进行一次过滤。使用\(z^o\)决定cell state的哪些部分将得到输出，将经过tanh过滤后的cell state与之结合得到我们期望的输出\(h^t\)。

那么LSTMs为什么会起作用？

首先要找到RNN失效的原因。RNN的每个单元包含两个输入：一个序列输入向量和一个hidden state，为了获得长序列中的语义，就要将很多RNN单元连接起来，最终得到一个深层网络。这样的一个深层网络可能带来两个问题，一个是所有深层网络都可能遇到的梯度爆炸问题，一个是长期依赖问题。梯度消失的原因不言自明，长期依赖问题值得关注，因为RNN中的状态传递像流水一般，逐层向下，不停的损失旧的状态和增加新的状态，在经过多层之后，对于之前的输入的记忆便会逐渐消失，如果此时需要用到较早的状态，那么在状态库中就找不到该状态了（例如，利用RNN做产品评价的情感分析，某评论为“我很喜欢xx产品，但是它还有一些不足……”，在RNN中很可能在捕获后面负面情感的时候已经“遗忘”了第一句中的很重要的正面情感而将该评论的情感误判）。为了解决这些问题，LSTM中引入了一个新的状态：cell state，用来进行长期记忆的任务，进而解决了长期依赖的问题。

下面推导下LSTM，就清楚为什么LSTM在cell state传递时没有梯度爆炸的问题了。

定义：

输入权重：\(\mathbf W_z,\mathbf W_i,\mathbf W_f,\mathbf W_o\in\mathbb R^{N\times M}\)

循环权重：\(\mathbf R_z,\mathbf R_i,\mathbf R_f,\mathbf R_o\in \mathbb R^{N\times N}\)

peephole权重：\(\mathbf p_i,\mathbf p_f,\mathbf p_o\in\mathbb R^N\)

bias权重：\(\mathbf b_z,\mathbf b_i,\mathbf b_o\in\mathbb R^N\)

前向传播： \(\begin{aligned}& block\ input: \begin{aligned} \bar{\mathbf z}^t & =\mathbf W_z\mathbf x^t+\mathbf R_z\mathbf y^{t-1}+\mathbf b_z \\ \mathbf z^t & = g(\bar{\mathbf z}^t) \end{aligned} \\& input\ gate: \begin{aligned} \bar{\mathbf i}^t & =\mathbf W_i\mathbf x^t+\mathbf R_i\mathbf y^{t-1}+ \mathbf p_i\odot\mathbf c^ {t-1} + \mathbf b_i \\ \mathbf i^t & = \sigma(\bar{\mathbf i^t}) \end{aligned} \\& forget\ gate: \begin{aligned} \bar{\mathbf f}^t & =\mathbf W_f\mathbf x^t+\mathbf R_f\mathbf y^{t-1}+ \mathbf p_f\odot\mathbf c^ {t-1} + \mathbf b_f \\ \mathbf f^t & = \sigma(\bar{\mathbf f^t}) \end{aligned} \\& cell state: \mathbf c^t=\mathbf z^t\odot \mathbf i^t+\mathbf c^{t-1}\odot \mathbf f^t \\& output gate: \begin{aligned} \bar{\mathbf o}^t & =\mathbf W_o\mathbf x^t+\mathbf R_o\mathbf y^{t-1}+ \mathbf p_o\odot\mathbf c^t + \mathbf b_o \\ \mathbf o^t & = \sigma(\bar{\mathbf o^t}) \end{aligned} \\& block\ output: \mathbf y^t = h(\mathbf c^t)\odot \mathbf o^t \end{aligned}\) \(\sigma\)为sigmoid，\(g\)和\(h\)都是tanh。

求导准备: \(\sigma(x)'=\sigma(x)(1-\sigma(x))\\ h(x)'=1-h(x)^2\)

反向传播：

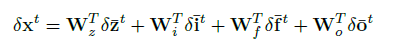
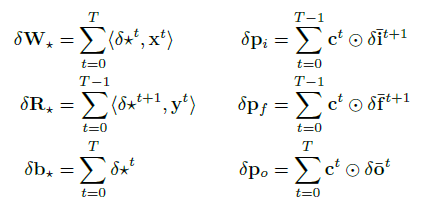
推导：

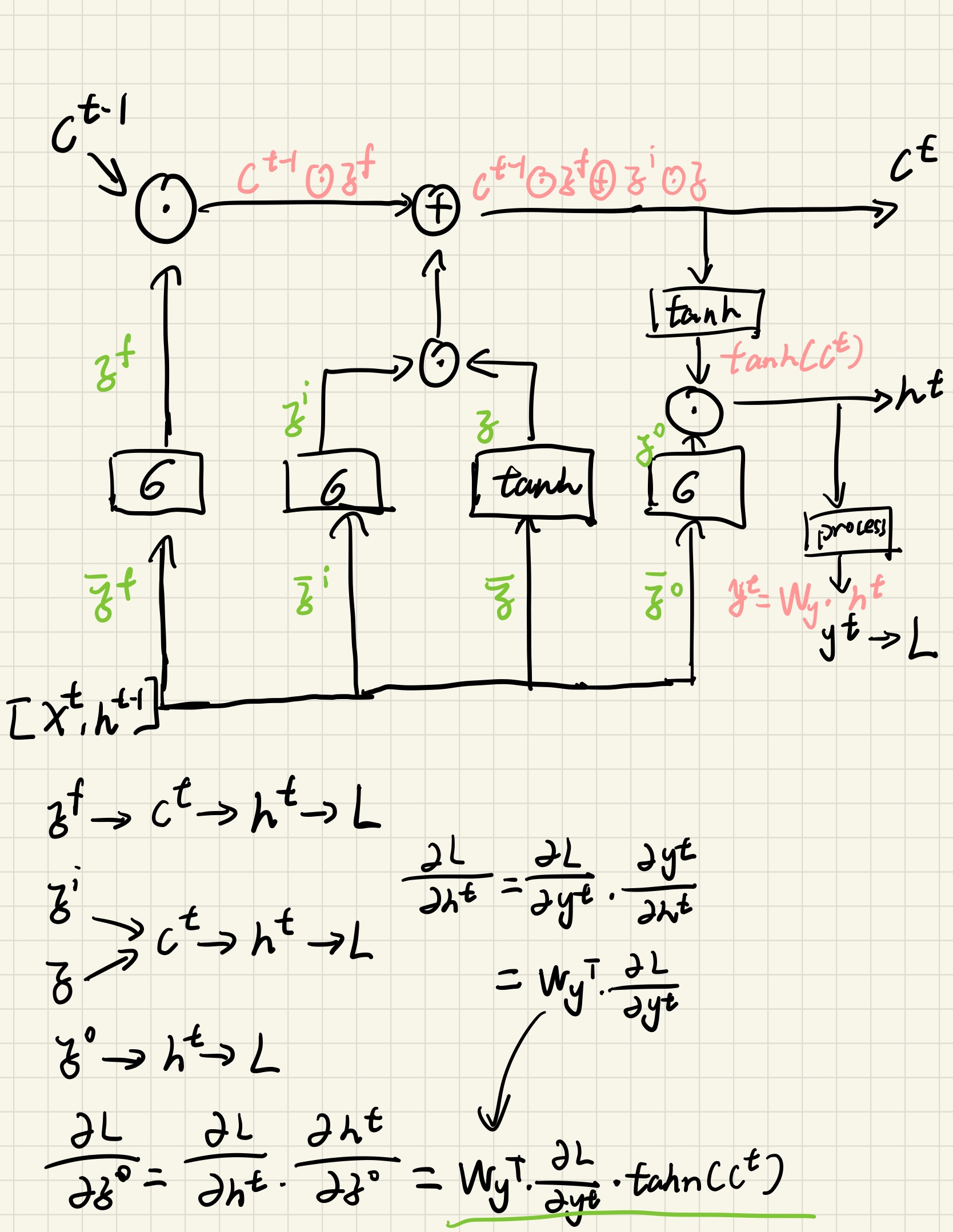
图中\(\odot\)为矩阵元素对应位置两两相乘（Hadamard Product）,\(\oplus\)为矩阵加法。

参考链接

[1] https://zhuanlan.zhihu.com/p/32085405

[2] http://colah.github.io/posts/2015-08-Understanding-LSTMs/

[3] https://zhuanlan.zhihu.com/p/125093069

[4] Greff K , Srivastava R K , Jan Koutník, et al. LSTM: A Search Space Odyssey[J]. IEEE Transactions on Neural Networks & Learning Systems, 2016, 28(10):2222-2232.