知识图谱学习

本文以《Introduction to Graph Neural Networks》为脉络，里面内容主要是摘自各类网上优秀作者（详情见参考资料）和笔者自己的思考。因为知识图谱的内容非常庞大，本文会不断更新。现在笔者的研究方向是基于时序知识图谱的预测，如有在这个方向的同行有兴趣交流，欢迎联系我 :)

这篇文章不包括时序图谱相关内容，时序知识图谱内容在另一篇文章内。

拉普拉斯矩阵

拉普拉斯矩阵，又称导纳矩阵，基尔霍夫矩阵或离散拉普拉斯。给定具有\(n\)个顶点的简单图\(G\)，其拉普拉斯矩阵\(L_{n\times n}\)定义为：

\[L=D-A\]

其中\(D\)是度矩阵，\(A\)是图的邻接矩阵。在\(L\)中，如果\(i=j\)，则元素为该节点的度；如果\(i\neq j\)且节点\(i\)和节点\(j\)相邻，则元素值为1。其余为0。

\(L\)有以下性质：

1. \(L\)是对称的
2. \(L\)是半正定的
3. \(L\)是一个\(M\)矩阵（自身的逆矩阵为一个非负矩阵）
4. \(L\)的每一行和列总和为0（对于无向图）

对称归一化拉普拉斯矩阵定义为： \(L^{sym}:=D^{-\frac{1}{2}}LD^{-\frac{1}{2}}=I-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\)

在\(L^{sym}\)中，如果\(i=j\)且度不为0，则元素为1；如果\(i\neq j\)且节点\(i\)和节点\(j\)相邻，则元素值为\(-\frac{1}{\sqrt{deg(v_i)deg(v_j)}}\)。其余为0。

随机游走归一化拉普拉斯矩阵定义为：

\[L^{rw}:=D^{-1}L=I-D^{-1}A\]

在\(L^{rw}\)中，如果\(i=j\)且度不为0，则元素为1；如果\(i\neq j\)且节点\(i\)和节点\(j\)相邻，则元素值为\(-\frac{1}{deg(v_i)}\)。其余为0。

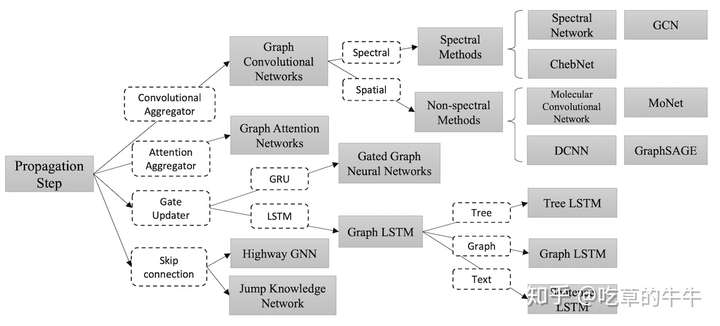
GNN

GNN的目的是为每个节点学习到一个状态embedding：\(h_v\in R^s\)，这个向量应该包括每个节点的邻居节点的信息，状态向量可以用于产生输出\(o_v\)。

假设\(f(\cdot)\)是带有参数的函数，称为局部转移函数（local transition function），这个函数在所有节点中共享，并根据邻居节点的输入来更新节点状态。假设\(g(\cdot)\)为局部输出函数（local output function），这个函数用于描述输出的产生方式。

\[h_v=f(x_v,x_{co[v]},h_{ne[v]},x_{ne[v]})\\ o_v=g(h_v,x_v)\]

\(x_v\)表示节点v的特征向量，\(x_{co[v]}\)表示与节点\(v\)关联的边的特征向量，\(h_{ne[v]}\)表示节点\(v\)的邻居节点的状态向量，\(x_{ne[v]}\)表示节点\(v\)的邻居节点特征向量。

将所有的向量表示为矩阵的形式，所有的状态向量\(H\)，所有的输出向量\(O\)，所有的特征向量\(X\)，所有的节点特征得到的向量\(X_N\)，得到全局转移函数和全局输出函数：

\[H=F(H,X)\\ O=G(H,X_N)\]

上式可以看出\(H\)是不动点，GNN使用传统迭代方法来计算状态参量：

\[H^{t+1}=F(H^t,X)\]

定义好GNN的框架之后，下一个问题就是学习函数\(f\)和\(g\)的参数，使用目标信息（\(t_v\)表示特定节点的标签）来进行监督学习，损失函数可以定义如下：

\[loss=\sum_{t=1}^p(t_i-o_i)\]

其中，\(p\)表示监督的节点数量，学习算法使用梯度下降法，整个过程按以下步骤：

1. 状态\(h_v^t\)按照迭代方程更新\(T\)个轮次，这时得到的\(H\)会接近不动点的解\(H(T)\approx H\)
2. 权重\(W\)的梯度从loss计算得到
3. 权重W根据上一步计算的梯度更新

有向图

DGP

Rethinking Knowledge Graph Propagation for Zero-Shot Learning,2018

DGP使用两种权重矩阵来获取更加精确的结构化信息，DGP的传播方式如下：

\[H^t=\sigma(D_p^{-1}A_p\sigma(D_c^{-1}A_cH^{t-1}W_c)W_p)\]

其中，\(D_p^{-1}A_p\)和\(D_c^{-1}A_c\)分别是双亲（parents）和后代（children）的归一化邻接矩阵。

异质图

异质图含有多种不同的节点种类，处理这种图最简单的方法是将每种节点的类型转化为One-hot特征向量，然后将One-hot向量和原始的节点特征进行连接，作为该节点的特征向量。

GraphInception

Deep Collective Classification in Heterogeneous Information Networks,2018

GraphInception提出将元路径（metapath）概念用在异质图的信息传播上，通过元路径的方式，可以根据节点类型和距离来对局部范围内节点进行分组，对于每一组，GraphInception将它作为异质图的一个子图，然后在子图内进行传播，并将不同异质图得到的结果进行连接得到综合的节点表示。

带有边信息的图

在这种图变体中，每一个边都带有额外的信息

G2S

Graph-to-Sequence Learning using Gated Graph Neural Networks,2018

将原始的图转化为一个二分图，处理方式为将原始的边转化为一个节点以及两条新的边，encoder使用如下的传播函数：

\[h^\prime_p=\rho(\frac{1}{\vert N_v\vert}\sum_{u\in N_v}W_r(r^t_v\odot h^{t-1}_u)+b_r)\]

其中，\(W_r\)和\(b_r\)是不同边类型的传播参数。

r-GCN

Modeling Relational Data with Graph Convolutional Networks,2017

在不同种类的边上，使用不同的权重矩阵进行传播的方式，也就是说，每一种边类型都关联一个权重矩阵，显然，对于边类型有很多的情况下，这种方式的参数量会非常大，r-GCN采用两种方法来减小参数。

图传播

卷积

为什么图卷积神经网络不能使用传统CNN？因为图谱是非欧式结构，不具有平移不变性，无法应用CNN中特定的size的卷积核对其进行特征提取。

卷积——频域

在所有这些频域方法中，学习得到的滤波器都是基于拉普拉斯特征分解，也就是取决于图的结构，这也就意味着，在一个特定结构上训练得到的模型，并不能直接应用到另外一个结构不同的图上。

利用谱方法的初衷是什么？将非欧式空间的图结构映射到欧式空间，再对投影之后的空间内的数据进行卷积，卷积之后的结果再还原到原来的空间。

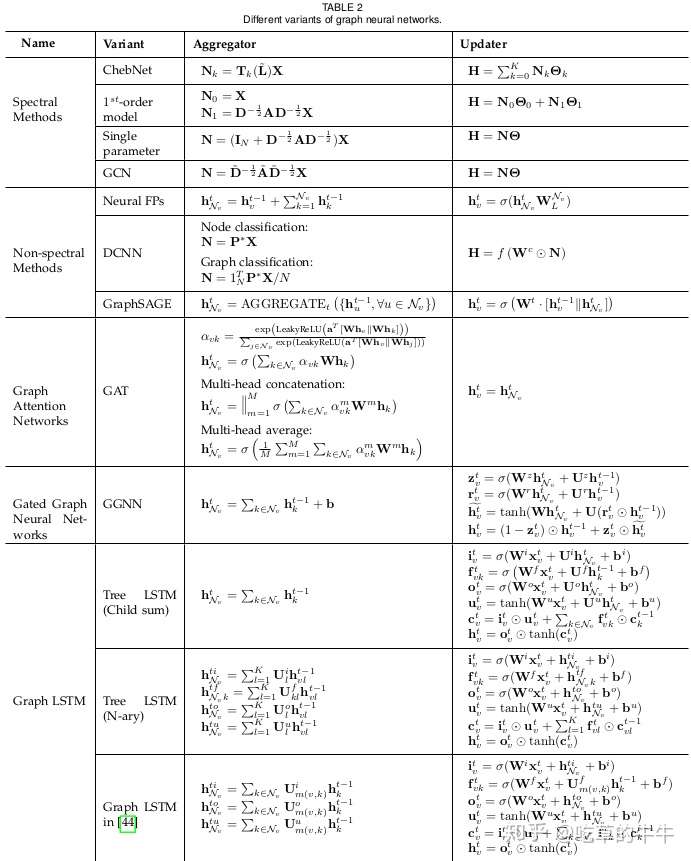
Spectral Network

Spectral Networks and Locally Connected Networks on Graphs,2013

将卷积操作定义为傅里叶频域计算图拉普拉斯的特征值分解。这个操作可以定义为使用卷积核\(g_\theta=diag(\theta)\)对输入\(x\in R^N\)（每一个节点有一个标量值）的卷积操作，其中\(\theta\in R^N\)：

\[g_\theta\star x=Ug_\theta(\Lambda)U^Tx\]

其中，\(U\)是标准化拉普拉斯矩阵\(L=I_N-D^{-\frac{1}{2}}AD^{-\frac{1}{2}}=U\Lambda U^T\)的特征向量矩阵，\(D\)是度矩阵（degree matrix），\(A\)是图的邻接矩阵，\(\Lambda\)为以特征值为对角线上的值的对角矩阵。这个操作会有比较高的计算量。

卷积核为特征值的函数，此处简单粗暴地使用参数：

\[g_\theta(\Lambda)= \left( \begin{array}{l} \hat{h}(\lambda_1) & & \\ & \ddots & \\ & & \hat{h}(\lambda_n) \end{array} \right)= \left( \begin{array}{l} \theta_1 & & \\ & \ddots & \\ & & \theta_n \end{array} \right)\]

如何通过傅里叶变换得到的？

已知\(L=U\Lambda U^T\)，使用\(U\)作为傅里叶变换的基底，将原特征投影到谱域中，有\(\widehat{x}=U^Tx\)，逆变换为\(x=U\widehat{x}\)，根据卷积定理，两个信号的卷积的傅里叶变换就是它们的傅里叶变换的点积，将GNN的卷积定义为：

\[x*_Gy=U((U^Tx)\odot(U^Ty))\]

其中\(y\)是卷积核函数，上式也就是先对\(x\)和\(y\)进行傅里叶变换，将变换结果（谱域中）进行卷积，再使用逆傅里叶变换回到原来的特征空间，式子可以简写为第一个式子的样子，拆开看：（1）\(U^Tx\)是对\(x\)做傅里叶变换（2）\(g_\theta(\Lambda)\)是卷积核（傅里叶变换之后）（3）\(g_\theta(\Lambda)U^Tx\)是傅里叶变换后的点积，相当于卷积后的傅里叶变换（4）\(U(g_\theta(\Lambda)U^Tx)\)中\(U\)就是逆傅里叶变换。

spectral network有以下弊端：

1. 拉普拉斯矩阵在遇到网络规模非常大的时候计算非常费力。
2. 与傅里叶基地相乘的时间复杂度太高，而且变到谱域之后还得变回来。
3. 信息更新来自于全局，而没有考虑局部邻居。

ChebNet

Convolutional Neural Networks on Graphs with Fast Localized Spectral Filtering,2016

使用谱方法对应的原始的卷积计算方式的时间复杂度是\(O(N^2)\)，复杂度较高。

用多项式代替卷积核

论文将\(\hat{h}(\lambda_l)\)巧妙地设计成了\(\sum_{j=0}^K \alpha_j\lambda_l^j\)，也就是：

\[g_\theta(\Lambda)= \left( \begin{array}{l} \sum_{j=0}^K \alpha_j\lambda_1^j & & \\ & \ddots & \\ & & \sum_{j=0}^K \alpha_j\lambda_n^j \end{array} \right)=\sum_{j=0}^K\alpha_j\Lambda^j\]

进而可以导出：

\[U\sum_{j=0}^K\alpha_j\Lambda^jU^T=\sum_{j=0}^K\alpha_jU\Lambda^jU^T=\sum_{j=0}^K\alpha_jL^j\]

用切比雪夫多项式代替卷积核

论文根据切比雪夫多项式定理，认为\(g_\theta(\Lambda)\)可以通过截取多项式的前\(K\)项来进行估计，因此有：

\[g_\theta\star x \approx U\sum_{k=0}^{K-1}\theta_k T_k(\tilde{\Lambda})U^Tx\\ = \sum_{k=0}^{K-1}\theta_k T_k(U\hat{\Lambda}U^T)x \\ = \sum_{k=0}^{K-1}\theta_k T_k(\hat{L})x\]

也就是有:

\[g_{\theta} =g_\theta(\Lambda)\approx\sum_{k=0}^{K-1} \theta_kT_k(\tilde \Lambda)\]

其中，\(\tilde{\Lambda}=\frac{2}{\lambda_{max}}\Lambda-I_N, \tilde{L}=\frac{2}{\lambda_{max}}L-I_N\)（这一步是re-scaled，因为切比雪夫多项式的输入在[-1,1]），\(\lambda_{max}\)表示矩阵\(L\)最大的特征值，\(\theta\in R^K\)为切比雪夫系数向量，切比雪夫多项式定义为：\(T_k(x)=2xT_{k-1}(x)-T_{k-2}(x)\)，且有\(T_0(x)=1,T_1(x)=x\)。可以看出这个操作是\(K-localized\)，因此在拉普拉斯中它是一个\(K\)阶多项式，由此避免了计算拉普拉斯的特征值。

利用卷积公式：

\[X^\prime=\sum_{k=1}^KZ^{(k)}\cdot\Theta^{(k)}\\ Z^{(1)}=X\\ Z^{(2)}=\widehat{L}\cdot X\\ Z^{(k)}=2\cdot\widehat{L}\cdot Z^{(k-1)}-Z^{(k-2)}\]

如果令\(K=1\)，chebnet的卷积公式就退化成了GCN，从另一个角度看，切比雪夫多项式的系数项就是图卷积的感受野。

GCN

Semi-Supervised Classification with Graph Convolutional Networks,2016

GCN限制了逐层的卷积操作，并设置\(K=1\)来减缓过拟合的问题，并且还近似了\(\lambda_{max}\approx2\)，最后简化的方程如下：

\[g_{\theta^\prime}\star x\approx \theta^\prime_0x+\theta^\prime_1(L-I_N)x=\theta^\prime_0x-\theta^\prime_1D^{-\frac{1}{2}}AD^{-\frac{1}{2}}x\]

使用两个无限制的参数\(\theta^\prime_0\)和\(\theta^\prime_1\)。在通过设置\(\theta=\theta^\prime_0=-\theta^\prime_1\)来限制参数的数量之后，可以得到以下的表达式：

\[g_\theta\star x\approx\theta(I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}})x\]

值得一提的是，叠加使用这个操作会导致数值不稳定性以及梯度爆炸或消失（因为不断地乘以同一个矩阵，因此，论文里使用了重规整化操作（renormalization））：

\[I_N+D^{-\frac{1}{2}}AD^{-\frac{1}{2}}\to\tilde{D}^{-\frac{1}{2}}\tilde{A}^{-\frac{1}{2}}\tilde{D}^{-\frac{1}{2}}\]

其中\(\tilde{A}=A+I_N\)，\(\tilde{D}_{ii}=\sum_j \tilde{A}_{ij}\)，最后论文将模型扩展为含有\(C\)个输入通道信号\(X\in R^{N\times C}\)以及\(F\)个滤波器来用于提取特征：

\[Z=\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}X\Theta\]

其中，\(\Theta\in R^{C\times F}\)是滤波器参数矩阵，\(Z\in R^{N\times F}\)是卷积信号矩阵。

卷积——空域

非频域的方法直接在图上定义卷积操作，也就是在空域上相邻的邻居节点上进行操作。这种非频域方法的主要难点在于如何定义拥有不同邻居数量的卷积操作以及保持CNN的局部不变性。

Neural FPs

Convolutional Networks on Graphs for Learning Molecular Fingerprints,2015

模型对不同度的节点使用不同的权重矩阵：

\[x=h^{t-1}_v+\sum_{i=1}^{\vert N_v\vert}h_i^{t-1}\\ h_v^t=\sigma(xW_t^{\vert N_v\vert})\]

其中，\(W_t^{N_v}\)是在第t层的度为\(\vert N_v\vert\)的节点的权重矩阵，这种方法的缺点在于不能应用到节点度比较大的graph上。

DCNN

Diffusion-Convolutional Neural Networks,2016

论文定义所有节点的特征矩阵定义为\(X_t\in R^{N_t\times F}\)，其中，\(N_t\)为图\(G_t\)的节点个数，\(F\)为节点特征维度。边信息\(E_t\)定义为\(A_t \in R^{N_t\times N_t}\)，由此可以计算出概率转移矩阵\(P_t\)（\(A_t\)中每个元素除以矩阵每行之和）。

模型将每一个预测的目标对象（节点、边或图）转化为一个diffusion-convolutional表示，大小为\(H\times F\)，\(H\)表示扩散的hops。

对于节点分类任务，\(P^*_t\)为一个\(N_t\times H\times N_t\)的张量，包含矩阵\(P\)的幂级数\(\{P_t,P^2_t,\dots,P^H_t \}\)，对于图\(t\)的节点\(i\)，第\(j\)个hop，第\(k\)维特征值\(Z_{tijk}\)计算公式为：

\[Z_{tijk}=f(W_{jk}^c\cdot \sum_{l=1}^{N_t}P^*_{tijl}X_{tlk})\]

矩阵形式为：

\[Z_t=f(W^c\odot P_t^*X_t),Z^t\in R^{N_t\times H\times F}\]

在计算出\(Z\)之后，过一层全连接得到输出\(Y\)，使用\(\hat{Y}\)表示分类结果，使用\(P(Y\vert X)\)表示预测概率，计算方法如下：

\[\hat{Y}=\arg\max(f(W^d\odot Z))\\ P(Y\vert X)=softmax(f(W^d\odot Z))\]

对于图分类任务，直接采用所有节点表示的均值作为graph的representation：

\[Z_t=f(W^c\odot 1^T_{N_t}P^*_tX_t/N_t)\]

对于边分类任务，通过将每一条边转化为一个节点来进行训练和预测，这个节点与原来的边对应的首尾节点相连，转化后的图的邻接矩阵\(A^\prime_t\)可以直接从原来的邻接矩阵增加一个关联矩阵得到：

\[A^\prime_t= \left( \begin{array}{l} A_t & B_t^T\\ B_t & 0 \end{array} \right)\]

DGCN

Dual graph convolutional networks for graph-based semisupervised classification,2018

论文提出了对偶图卷积网络，同时考虑到图上的局部一致性和全局一致性，使用两组卷积网络来获取局部/全局的一致性，并使用一个无监督的loss来组合它们，第一个卷积网络和方程相同，第二个卷积网络将邻接矩阵替换为PPMI（positive pointwise mutual information）

局部一致性

对于局部一致性，论文直接使用了\(K=1\)的ChebNet：

\[Z^{(i)}=Conv_A^{(i)}(X)=\sigma(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}Z^{(i-1)}W^{(i)})\]

但是，对于图结构数据而言，不相似节点可能直接相连，也就是连通节点之间的相似度可能低于未连通节点。对于这种情况1stChebNet模型无法处理，它对节点的邻域信息进行聚合时需要保证相邻节点的特征相似。所以作者引入了全局一致性卷积来解决这个问题。

全局一致性

作者设计通过概率统计的方式获取了一种新的可以代表图的结构信息的频率矩阵\(F\)，利用逐点互信息的方法构建了PPMI矩阵。每个节点的转移概率可以有下式得到：

\[p(s(t+1)=x_i\vert s(t)=x_i)=A_{ij}/\sum_jA_{ij}\]

获得频率矩阵\(F\)：

1. 确定节点的随机游走长度\(\gamma\)，采样次数\(w\)，初始化频率矩阵\(F\)值为0。
2. 以节点\(x_i\)为起点，开始以0为步长随机游走，得到所有可能的情况，表示为点对集合\(S=\{(x_n,x_m)\}\)，接着以上述等式作为概率采样\(w\)次，得到\(w\)个对点对。
3. 对于点对\((x_n,x_m)\)，在频率矩阵中对应位置\(F_{n,m},F_{m,n}\)对应加1。
4. 将游走步长逐渐变化到\(\gamma\)，循环（2）（3）步骤。
5. 对于所有的节点，执行（2）（3）（4）得到频率矩阵\(F\)。

在构建矩阵\(F\)完成后，构建PPMI矩阵\(P\)。

节点\(i,j\)之间扩散的概率为：

\[p(ij)=p_{ij}=\frac{F_{i,j}}{\sum_{i,j}F_{i,j}}\]

从节点\(i\)开始扩散的边缘概率为：

\[p(i)=p_{i,*}=\frac{\sum_jF_{i,j}}{\sum_{i,j}F_{i,j}}\]

扩散到节点\(j\)的边缘概率为：

\[p(j)=p_{*,j}=\frac{\sum_iF_{i,j}}{\sum_{i,j}F_{i,j}}\]

通过使得不相关和负相关的PMI值都为0，得到矩阵\(P\)：

\[P_{i,j}=max\{pmi_{i,j}=log(\frac{p_{i,j}}{p_{i,*}p_{*,j}}),0 \}\]

将矩阵\(P\)作为邻接矩阵，带入1stChebNet模型：

\[Z^{(i)}=Conv_P^{(i)}(X)=\sigma(D^{-\frac{1}{2}} P D^{-\frac{1}{2}}Z^{(i-1)}W^{(i)})\]

其中，\(Conv_A,Conv_p\)是共享权重的，即训练参数\(W^{(i)}\)是一样的。

整合一致性

由于缺少训练数据（半监督训练，只有少量有标签的节点），无法利用通常的类似直接拼接两个输出的方法对结果进行集成，否则得到的性能将会很差。所以作者提出了利用无监督的方法对这两个输出进行整合。

对于局部一致性卷积的结果\(Conv_A^{(i)}(X)\)，使用传统有标签的交叉熵损失：

\[L_0(Conv_A)=-\frac{1}{y_L}\sum_{l\in y_L}\sum_{i=1}^CY_{l,i}ln\hat{Z}_{l,i}^A\]

其中，\(y_L\)表示有标签节点集合，\(c\)为分类种数，\(Y_{l,i}\)为节点\(l\)的标签，\(\hat{Z}_{l,i}^A\)表示节点的预测结果。

对于全局一致性卷积的结果\(Conv_P^{(i)}(X)\)：虽然\(A,P\)矩阵不一样，但最后的预测结果需要异质，所以可以采用均方差作为损失，将局部和全局一致性进行整合：

\[L_{reg}(Conv_A,Conv_p)=\frac{1}{n}\sum_{i=1}^n\Vert \hat{Z}_{l,i}^A - \hat{Z}_{l,i}^P\Vert^2\]

最后损失函数为：

\[L=L_0(Conv_A)+\lambda(t)L_{reg}(Conv_A,Conv_p)\]

其中，\(\lambda(t)\)为动态权重，\(t\)表示时间。在刚开始是\(t\)比较小，损失函数由\(L_0(Conv_A)\)主导，通过\(L_0(Conv_A)\)损失获得后验分布；随着时间的推移，\(\lambda(t)\)增大，\(L_{reg}(Conv_A,Conv_p)\)开始对模型参数产生影响，将同时考虑两者。这样的动态权值可以加速模型的收敛，同时使得参数可以收敛到正确的解上。

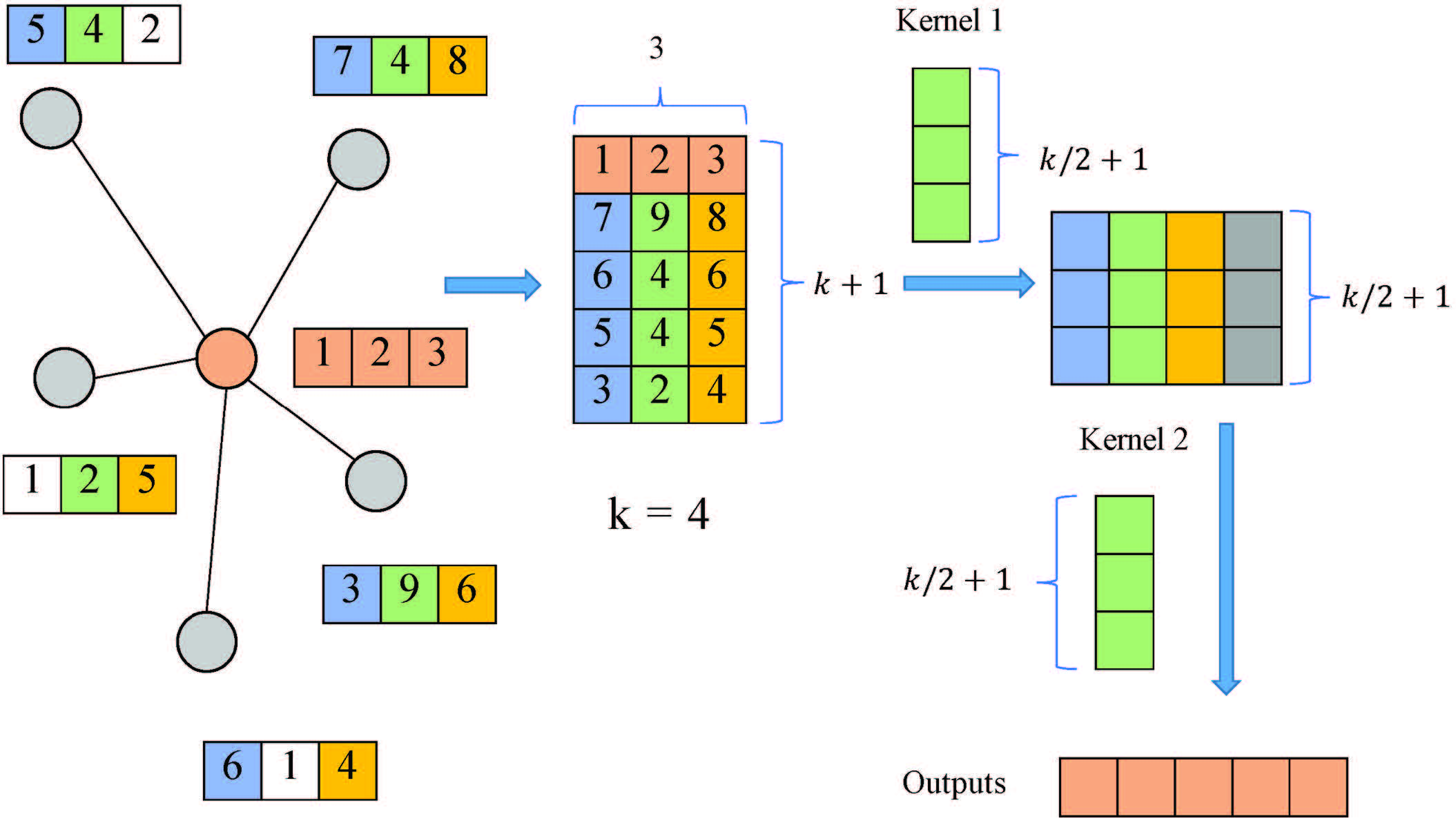
LGCN

Large-scale learnable graph convolutional networks,2018

LGCN基于LGCL（learnable graph convolutional layer）和子图训练策略。

LGCL

LGCL的layer-wise传播规则遵循LGCL的定义，传播规则为：

\[\hat{X}_l=g(X_l,A,k)\\ X_{l+1}=c(\hat{X}_l)\]

其中\(g(\cdot)\)是一个k-largest Node Selection函数，将图结构数据映射到网格结构，\(c(\cdot)\)表示1维CNN，将顶点信息聚合，为每个顶点输出一个新的特征向量。具体来说，LGCL的作用是将原来的非欧结构的图结构变为一维网格结构，这样可以用于卷积网络。GCN的做法是使用1stchetnet，但这样做的结果是\(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}\)中没有可供训练的参数，另外，每个相邻的节点在加权和中得到相同的权重，这使得它成为一个简单的平均值，GCN中不可训练的聚合操作限制了GCNs对通用图数据的能力。

k-largest Node Selection

对于图，有\(X_l\in R^{N\times C}\)，其中\(N\)为节点数，\(C\)为特征数，每个行向量记为\(x^i_l\)，对于\(x^i_l\)有\(n\)个邻居，分别为\(i_1,i_2,\dots,i_n\)，将所有邻居的特征向量进行拼接，得到\(M^i_l\in R^{n\times C}\)，假设\(n\geq k\)，那么直接取\(k\)；假设\(n<k\)，那么下面操作时使用全0padding。对\(M_l^i\)的每一列，排序完取最大的\(k\)个数（有点像max pooling），得到一个\(k\times C\)的输出矩阵，在第一行插入\(x_l^i\)，得到\(\tilde{M}_l^i\in R^{(k+1)\times C}\)。对每个顶点进行如此操作，\(g(\cdot)\) 将\(X_l\)变为了\(\tilde{X}_l\in R^{N\times(k+1)\times C}\)。

MONET

论文使用\(x\)表示图谱中的节点，\(y\in N_x\)表示\(x\)的邻居节点。MONET使用一个权重方程去计算由节点和节点邻居组成的伪坐标（pseudo-coordinate）\(u(x,y)\)：

\[D_j(x)f=\sum_{y\in N_x}w_j(u(x,y))f(y)\]

其中，参数为\(w_\Theta(u)=(w_1(u),\dots,w_J(u))\)并且\(J\)表示抽取出路径的规模。一个基于空域的非欧领域的卷积就可以定义为：

\[(f\star g)(x)=\sum_{j=1}^Jg_jD_j(x)f\]

其他方法都可以认为是特例：

GraphSAGE

GraphSAGE：Inductive Representation Learning on Large Graphs,2017

论文提出了一个一般的归纳框架，这个框架通过从一个节点的局部邻居中采用和聚合特征，来产生节点的embedding：

\[h^t_{N_v}=AGGREGATE_t(\{h_u^{t-1},\forall u\in N_v \})\\ h^t_u=\sigma(W^t\cdot[h_v^{t-1}\Vert h_{N_v}^t])\]

但是，上述的方程并不会采用所有的邻居节点进行计算，而是使用均匀采样来得到固定大小的邻居节点集合，该论文推荐使用三种聚合函数：

（1）平均值聚合：

\[h_v^t=\sigma(W\cdot MEAN(\{h_v^{t-1} \}\cup\{h_u^{t-1} ,\forall u\in N_v \})\]

平均值聚合和其他的聚合方式不同，因为它不用进行连接操作。

（2）LSTM聚合：

基于LSTM的聚合器有更好的表达能力，然而，LSTM以序列的方式顺序地处理输入，因此，它并没有排列不变性，论文采用重排列节点邻居地方式，在无序集合中使用LSTM操作。

（3）池化聚合：

每一个邻居的隐藏状态输入到一个全连接欸曾，然后使用最大池化操作应用到邻居节点集合：

\[h_{N_v}^t=max(\{\sigma(W_{pool}h_u^{t-1}+b),\forall u\in N_v\})\]

另外，任何对称的函数都可以用来替换这里的最大池化操作。

门机制（Gate）

目前在信息传播步骤中使用的门机制类似于GRU和LSTM模型，这种机制可以减少原始GNN模型的约束，并提升在图结构中的长期的信息传播。

GGNN

GATED GRAPH SEQUENCE NEURAL NETWORKS,2016

论文提出了门控图神经网络（GGNN），在信息传播步骤中使用GRU，将递归循环展开固定数量的步数，并使用按照时间序的反向传播来计算梯度。具体来说，传播的基本递归循环如下：

按照第一个公式，节点\(v\)首先从它的邻居节点汇集信息，其中，\(A_u\)为图邻接矩阵\(A\)的子矩阵，表示节点\(v\)和它的邻居节点的连接关系。然后，类似于GRU的节点更新函数将该节点前一个时刻的信息与该节点相邻的其他节点的信息结合起来，以此来更新每一个节点的隐藏状态。\(a\)汇集了节点\(v\)周围节点的信息，\(z\)和\(r\)分别是更新门和重置门。

Tree-LSTM

Improved Semantic Representations From Tree-Structured Long Short-Term Memory Networks,2015

论文提出了两个LSTM的扩展结构，Child-Sum Tree-LSTM和N-ary Tree-LSTM，类似于标准的LSTM单元，每一个Tree-LSTM单元（为）包含输入门（input gate）和输出门（output gate），记忆单元（memory cell）和隐藏状态（hidden state），但与LSTM（LSTM单元只包含一个遗忘门）不同的是，Tree-LSTM单元对每一个孩子节点都有一个遗忘门，这样就可以从孩子节点中选择性地汇集并组合信息。

注意力机制

GAT

Graph Attention Networks,2018

论文提出了图注意力网络，将注意力机制引入到信息传播步骤，这个模型通过对它的邻居节点增加注意力来注意节点的隐藏状态（和self-attention策略类似）。该论文定义了一个graph attentional layer，并通过叠加这种层来构建任意的图注意力网络，这个层计算节点对\((i,j)\)的注意力系数（coefficients），计算方法如下：

\[a_{ij}=\frac{\exp(Leaky\ ReLU(a^T[Wh_i][Wh_j]))}{\sum_{k\in N_i}\exp(Leaky\ ReLU(a^T[ Wh_i][Wh_k]))}\]

其中，\(a_{ij}\)是节点\(j\)对\(i\)的注意力系数，\(N_i\)表示图中节点\(i\)的邻居节点集合，节点特征的输入集合是\(h=\{h_1,h_2,\dots,h_N \}h_i\in R^F\)，其中\(N\)是节点的个数，\(F\)是每个节点的特征维度。这个层会产生一个新的节点特征集：\(h^\prime=\{h^\prime_1,h^\prime_2,\dots,h^\prime_N \}h^\prime_i\in R^{F^\prime}\)，作为该层的输出，\(W\in R^{F^\prime \times F}\)是共享的线性变换的权重矩阵，\(a\in R^{2F^\prime}\)是单层的前向神经网络的权重向量，通过softmax函数对它进行归一化，然后使用LeakyReLU（\(\alpha=0.2\)）非线性函数。

每个节点的输出特征如下：

\[h^\prime_i=\sigma(\sum_{j\in N_i}\alpha_{ij}Wh_j)\]

对于注意力模型，可以使用多头注意力来适得网络学习过程更加稳定。

这篇论文的注意力机制结构有如下几个特点：(1)node-neighbor pair的计算可以是并行化的，因此操作的效率高；(2)通过给邻居节点赋予任意的权重，可以用在有不同度的图节点上；(3)可以容易地用于归纳学习问题上。

跳过连接（Skip connection）

许多应用都会将图神经网络层进行叠加，以此来实现更好的结果，因为更多的层意味着每一个节点能够从更多的邻居节点中获取信息，但是，许多实验发现，更深的模型并不会表现更好，反而可能表现更坏，主要因为随着指数个数上升的相邻节点数量，更多的层可能会汇集到更多的噪声信息。一个直接的想法是使用残差网络(residual network)，但是即使使用残差连接，有更多层的GCN在很多数据上并没有2层的GCN表现的更好。

Highway GCN

Highway Networks,2015

论文使用类似于highway network的方法，使用了“逐层门机制”。

分层池化（Hierarchical Pooling）

在计算机视觉中，一个卷积层后通常会接一个池化层，来得到更加一般的特征。与这种池化层类似的是，在图结构中，一种分层池化层也能够起到类似的效果，复杂的和大规模的图通常会包含丰富的分层结构，这种结构对于节点层次(node-level)和图层次(graph-level)的分类任务非常重要。

参考资料

GNN综述：Review of Methods and Applications - 知乎 (zhihu.com)

谱卷积的GNN原理解释（Spectral Network），附代码_五月的echo的博客-CSDN博客

chebnet介绍与实现_Yichar的博客-CSDN博客_chebnet

如何理解 Graph Convolutional Network（GCN）？ - 知乎 (zhihu.com)

GNN模型：Diffusion-Convolutional Neural Networks - 知乎 (zhihu.com)

《Dual Graph Convolutional Networks for Graph-Based Semi-Supervised Classification》论文理解_moster.YC的博客-CSDN博客

LGCN论文笔记]：Large-Scale Learnable Graph Convolutional Networks_知行合一，止于至善-CSDN博客

20ICLR 多关系图神经网络 CompGCN - 知乎 (zhihu.com)