读 Knowledge Graph Embedding: A Survey of Approaches and Applications

update:2019.11.28 写到了3.2.2之前

update:2019.11.29 模型对比

update:2020.5.15 修改了部分错别字，增加了一部分补充内容

---

预先定义 $定义\circ:\mathbb R^n \times \mathbb R^n\rightarrow \mathbb R^n表示Hadamard乘积\\ [a\circ b]_i = [a]_i\cdot [b]i,\\ 定义\star:\mathbb R^n \times \mathbb R^n\rightarrow \mathbb R^n表示circular correlation\\ [a\star b]_i = \sum_{k=0}^{n-1}[a]_k\cdot[b]_{(k+i)\ mod\ n}.$

---

$$D^+={(h,r,t)}关系三元组\\ h,t \in \mathbb E;r\in \mathbb R$$

E是entity（实体）的集合，R是relation（关系）的集合。

一般来说，将知识图谱向量划分为三步：

1. 将entity和relation替换为向量的形式
2. 定义score function用来评估，f_r(h,t)表示实体h到实体t通过关系r的合理性
3. 学习过程，使得f_r(h,t)的和最大

有两种embedding technique技巧，一种是translational distance models，一种是semantic matching models。

---

Translational Distance Models

TransE及其拓展

TransE

h,r,t都是$R^d$的向量，可以认为$\textbf h+\textbf r \approx \textbf t$，于是有

$$f_{r}(h,t)=-\left\|h+r-t\right\|_{1/2}(1/2表示第一或第二范式).$$

但是，以上式子有个缺陷，面对1-to-N，N-to-1，N-to-N的问题时，彼此相关性不大但是和某实体具有相同关系的实体之间的embedding很接近。因此有一些TransE的改良版本。

TransH（Hyperplanes）

对于每个关系r，都有一个r与之对应，和之前的方法不同的是，这个r位于一个超平面，其法向量为w_r。对于每个事实(h,r,t)，将其实体对应的向量h和t首先投影到超平面，有

$h_\perp=h-w_r^Thw_r,\ t_\perp=t-w_r^Ttw_r$，同上也就有$\textbf h_\perp+\textbf r \approx \textbf t_\perp$此时$f_{r}(h,t)=-\left\|h_\perp+r-t_\perp\right\|_2^2$，TransH允许一个实体在不同的关系中有各自的角色，同时不同实体在同一关系中的意义也可以相同

TransR（Relation-specific）

与TransH类似，但是引入了一个relation-specific空间，而不是使用超平面，实体均属于$R^d$空间，而每个关系与一个$R^k$空间联系，并且用一个转换向量来表示，给定一个事实(h,r,t)，TranR首先对实体表示的向量进行投影，有

$h_\perp=M_rh,\ t_\perp=M_rt.\ 其中M_r\in \mathbb R^{k\times d}$,M_r是一个投影矩阵，将实体空间投影到r的关系空间，此时$f_r(h,t)=-\left\|h_\perp+r-t_\perp\right\|_2^2$，与TransH相比，对于复杂关系的处理更强了，可以将在实体空间中接近但不是同属于一个关系的实体分开，但是需要的参数更多（需要$d \times k$的矩阵，O(dk)）

TransD

TransD通过将投影矩阵分解来简化了TransR，对于每个事实(h,r,t)，TransD增加了三个映射向量$w_h,w_t\in \mathbb R^d;w_r\in \mathbb R^k$。有两个投影矩阵$M_r^1,M_r^2$定义为

$$M_r^1=w_rw_h^T+I,\ M_r^2=w_rw_t^T+I.$$

将两个矩阵分别应用于h和t，有

$$h_\perp=M_r^1h,\ t_\perp=M_r^2t.$$

score funciton与TransR相同

TransSparse

TransSparse通过对投影矩阵稀疏化来简化TransR，有两个版本。

TranSparse（share）用同一个稀疏投影矩阵$M_r(\theta_r)$

$$h_\perp=M_r(\theta_r)h,\ t_\perp=M_r(\theta_r)t.$$

TransSparse（separate）对head和tail用不同的矩阵

$$h_\perp=M_r^1(\theta_r^1)h, t_\perp=M_r^2(\theta_r^2)t.$$

这里$\theta_r,\theta_r^1,\theta_r^2$表示对于投影矩阵不同的稀疏度（通过对矩阵增0的方法减少需要的参数），score funciton与TransR相同

TransM

对于TransE，有个严格约束$\textbf h+\textbf r \approx \textbf t$，TransM通过给每个事实一个权重$\theta_r$来放松约束，也就是说允许h+r离t更远，现在score function为

$$f_{r}(h,t)=-\theta_r\left\|h+r-t\right\|_{1/2}.$$

对1-to-N，N-to-1，N-to-N的情况给予较低的权重。

ManifoldE

ManifoldE将$\textbf h+\textbf r \approx \textbf t$转换为$\left\|h+t-r\right\|_2^2 \approx\theta_r^2$，同样放松了对于约束的要求，使得t能在一个流形（manifold）上得到近似，一个以h+r为中心，$\theta_r$为半径的超球面，以代替原来的直接的对h+r的近似，现在的score function为

$$f_{r}(h,t)=-(\left\|h+r-t\right\|_2^2-\theta_r^2)^2.$$

TransF

TransF通过使t分布在与h+r的相同方向上来放松约束，同时，h也在t-r的相同方向上，现在的score function为

$$f_r(h,t)=(h+r)^Tt+(t-r)^Th.$$

TransA

TransA对每个关系r使用一个对称非负矩阵$M_r$，此时的socre function为（使用马氏距离，TransE降维之后是一个圆形，TransA降维之后是一个椭圆）

$$f_r(h,t)=-(\left|h+r-t\right|)^TM_r(\left|h+r-t\right|).$$

通过对$M_r$的学习，TransA对于复杂关系的处理更灵活。

---

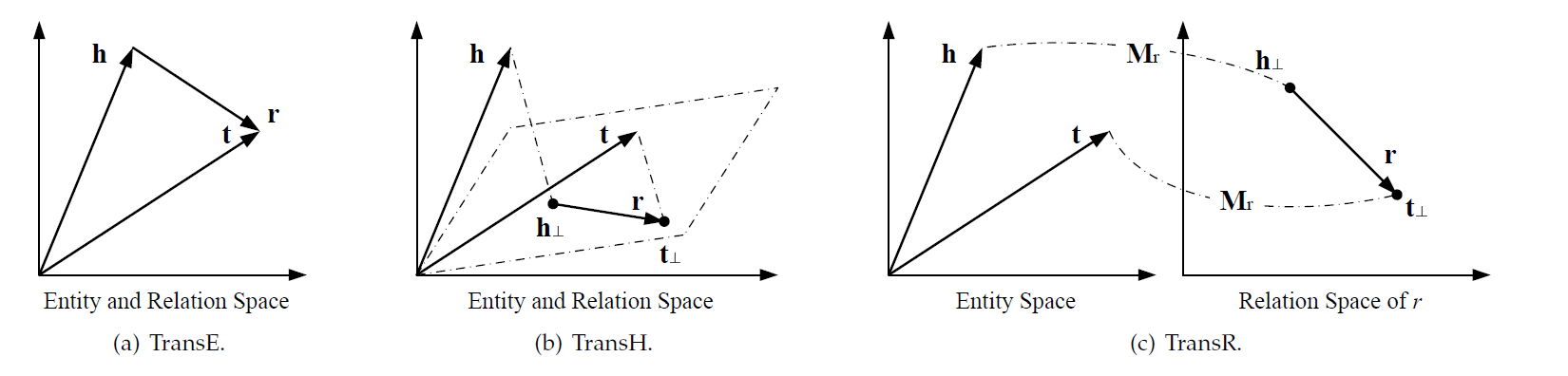
TransE及其拓展图示

---

GussianEmbeddings

KG2E

考虑到实体和关系的不确定性，将h,t,r都视为多元高斯分布。

$$h\sim\mathcal N(\mu_h,\sum h),\\ t\sim\mathcal N(\mu_t,\sum t),\\ r\sim\mathcal N(\mu_r,\sum r),\\其中\mu_h,\mu_t,\mu_r \in \mathbb R^d;\sum h,\sum t,\sum r\in \mathbb R^{d\times d}(协方差矩阵).$$

通过衡量t-h与r之间的距离来对结果打分，也就是对应的$\mathcal N(\mu_t-\mu_h,\sum t+ \sum h)和\mathcal N(\mu_r,\sum r)$

基于此，有两种score function

Kullback-Leibler divergence

$$f_r(h,t)=-\int\mathcal N_X(\mu_t-\mu_h,\sum t+\sum h)\ln\frac{\mathcal N_X(\mu_t-\mu_h,\sum t + \sum h)}{\mathcal N_X(\mu_r,\sum r)}dX\\\propto-tr(\sum\nolimits^{-1}_r(\sum h+\sum t))-\mu^T\sum\nolimits^{-1}_r\mu-\ln\frac{\det(\sum r)}{\det(\sum h)+\sum t)}.$$

probability inner product

$$f_r(h,t)=\int \mathcal N_X(\mu_t-\mu_h,\sum t + \sum h)\cdot\mathcal N_X(\mu_r,\sum_r)dX\\\propto-\mu^T\sum\nolimits^{-1}\mu-\ln(\det(\sum)).$$

其中，$\mu=\mu_h+\mu_r-\mu_t;\sum=\sum h + \sum r + \sum t$，Gaussian embeddings对于实体和关系的不确定性处理很有效。

TransG

同样将实体是为高斯分布

$$h\sim\mathcal N(\mu_h,\sigma_h^2I),\ t\sim\mathcal N(\mu_t,\sigma_t^2I).$$

假设每个关系可能有多重的语义（比如英文中的has part可以表示composition【组成部分】，也可以表示location【位置从属】），那么关系就应该服从混合高斯分布

$$r=\sum_i\pi_r^i\mu_r^i,\ \mu_r^i\sim\mathcal N(\mu_t-\mu_h,(\sigma_h^2+\sigma_t^2)I).$$

这里，$\mu_r^i$表示第i个语义，$\pi_r^i$是其对应权重，现在，socre function为

$$f_r(h,t)=\sum_i\pi_r^i\exp\left(\frac{-\left\|\mu_h+\mu_r^i-\mu_t\right\|_2^2}{\sigma_h^2+\sigma_t^2}\right).$$

Other Distance Models

UM（Unstructured Model）

相对TransE来说，UM是一种不成熟的模型，它将所有的r设为0，其socre function为

$$f_r(h,t)=-\left\|h-t\right\|_2^2.$$

显然，这样无法区分不同的关系。

SE（Structured embedding）

SE使用了两个单独的矩阵$M_r^1和M_r^2$来分别对h和t投影，有

$$f_r(h,t)=-\left\|M_r^1h-M_r^2t\right\|_1.$$

---

Translational Distance Models的对比

---

---

Semetic Matching Models

semantic matching models采用基于相似性的score function，通过衡量实体与关系的向量空间中的潜在语义关系来做为评判的标准。

RESCAL及其拓展

RESCAL

RESCAL是一个双线性模型（双线性模型可以更好的去拟合非线性关系），每个实体是一个向量（包含其潜在的语义），每个关系是一个矩阵，这个矩阵根据每对潜在的实体进行建模，其score function为

$$f_r(h,t)=h^TM_rt=\sum_{i=0}^{d-1}\sum_{j=0}^{d-1}[M_r]_{ij}\cdot[h]_i\cdot[t]_j,\\h,t\in \mathbb R^d,M_r\in \mathbb R^{d\times d}$$

对$M_r$分解还可以减少涉及的参数

$$M_r=\sum\nolimits_i\pi_r^iu_iv_i^T(将M_r分解为一组秩为1的矩阵)$$

TATEC

引入更多的因子来扩充score function，

$$f_r(h,t)=h^TM_rt+h^Tr+t^Tr+h^TDt，D是对角矩阵$$

DistMult

DistMult通过规定$M_r$为对角矩阵,对于每个关系r，有向量r与之对应，并且要求$M_r=diag(r)$，现在，score function为

$$f_r(h,t)=h^Tdiag(r)t=\sum_{i=0}^{d-1}[r]_i\cdot[h]_i\cdot[t]_i.$$

但是，因为$h^Tdiag(r)t=t^Tdiag(r)h$，这个过于简化的模型可能导致生成KGs模型的说服力不足。

Holographic Embeddings（HolE）

HolE结合了RESCAL表现力强的特点和DistMult的简易性，它将实体与关系都表示为$R^d$内的向量。给定一个事实(h,r,t)，实体先被分解为$h\star t\in R^d$，现在score function为

$$f_r(h,t)=r^T(h\star t)=\sum_{i=0}^{d-1}[r]_i\sum_{i=0}^{d-1}[h]_k\cdot [t]_{(k+i)\ mod \ d}.$$

circular correlation 相当于对每对实体进行了一次压缩，并且注意$h\star t \neq t\star h$，因此HolE可以对非对称关系建模（与RESCAL一样）

Complex Embeddings（ComplEx）

ComplEx通过引入复值向量来优化DistMult无法处理非对称关系的问题。在这个基础上，h,r,t不再属于实数空间而是属于复数空间（记为$C^d$）,现在score function为

$$f_r(h,t)=Re(h^Tdiag(r)\bar t)=Re(\sum_{i=0}^{d-1}[r]_i\cdot[h]_i\cdot[\bar t]_i),\\ 其中，\bar t是t的共轭，Re(\cdot)是选取复数的实数部分。$$

这样一来，就可以解决DistMult中的非对称关系问题。研究表明，每个ComplEx都有一个HolE等式，HolE是ComplEx中的一个特殊情况

ANALOGY

ANALOGY采取与RESCAL相似的score function，

$$f_r(h,t)=h^TM_rt=\sum_{i=0}^{d-1}\sum_{j=0}^{d-1}[M_r]_{ij}\cdot[h]_i\cdot[t]_j,\\h,t\in \mathbb R^d,M_r\in \mathbb R^{d\times d}$$

再此基础上，它要求关系的线性映射矩阵$M_r$必须是正规的和可交换的，即

$$normality(正规):M_rM_r^T=M_r^TM_r,\forall r\in \mathbb R\\ commutativity(可交换):M_rM_{\acute r}=M_{\acute r}M_r,\forall r,\acute r\in \mathbb R.$$

以上的DistMult，HolE，ComplEx原则上都可以看为是ANALOGY的特殊情况

---

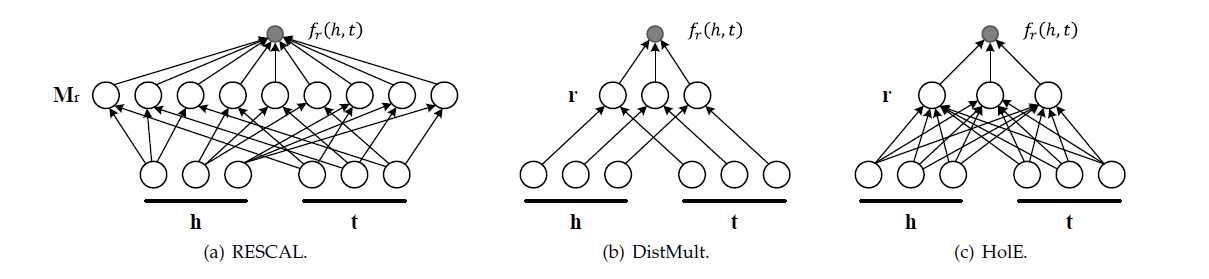
RESCAL及其拓展

---

Matching with Neural Networks

Semantic Matching Energy（SME）

利用神经网络进行语义的匹配，给定一个事实(h,r,t)，首先将它的实体和关系在输入层投影为向量。然后在隐藏层将h与r融合，得到$g_u(h,r)$，同理，将t与r融合，得到$g_v(t,r)$，将score function定义为他们的点积

$$f_r(h,t)=g_u(h,r)^Tg_v(t,r)$$

对于$g_u$与$g_v$有两种表示形式，包括线性的和双线性的。

linear：

$$g_u(h,r)=M_u^1h+M_u^2r+b_u,\\g_v(t,r)=M_v^1t+M_v^2+b_v.$$

bilinear:

$$g_u(h,r)=(M_u^1h)\circ(M_u^2r)+b_u,\\g_v(t,r)=(M_v^1t)\circ(M_v^2r)+b_v.\\其中，M_u^1,M_u^2,M_v^1,M_u^2\in \mathbb R^{d\times d}(权重矩阵)\\b_u,b_v\in \mathbb R^d(偏置向量)$$

Nerual Tensor Network（NTN）

用一个双线性张量层代替一个标准的线性神经网络层，它直接关联了多个维度上的两个实体向量。首先将实体映射为d维向量，然后用一个关系特化的张量$\underline M_r\in R^{d\times d \times k}$将其映射到一个非线性的隐藏层，最后用一个关系特化的输出层给出分数，激活函数为双曲正切函数，score function为

$$f_r(h,t)=r^T\tanh(h^T\underline M_rt + M_r^1h+M_r^2t+b_r),\\其中，M_r^1,M_r^2\in \mathbb R^{k \times d};b_r\in \mathbb R^k$$

$h_T\underline M_rt$的结果是一个向量，第i条数据的计算方式为$h_T\underline M_r^{[:,:,i]}t$。

通过设置$\underline M_r = 0,b_r=0$NTN可以简化为单层模型SLM，NTN应该是迄今（论文发表时）最具有表现力的模型，但是涉及的参数较多，效率较低。

Multi-Layer Perception

利用多层感知机，将实体和关系表示为向量作为输入，输入到一层非线性隐藏层，score function为

$$f_r(h,t)=w^T\tanh(M^1h+M^2r+M^3t)\\其中，M^1,M^2,M^3\in \mathbb R^{d\times d}(第一层的权重)\\w\in \mathbb R^d(第二层的权重).$$

Neural Association Model（NAM）

利用深层神经网络，给定一个事实(h,r,t)，首先将head实体与关系拼接作为输入层，有$z^{(0)}=[h;r]\in R^{2d}$，然后把输入$z^{(0)}$输入进由L个线性整流函数（ReLU）组成的深层神经网络，有

$$a^{(l)}=M^{(l)}z^{(l-1)}+b^{(l)},\ l=1,\cdots,L,\\z^{(l)}=ReLU(a^{(l)}),\ l=1,\cdots,L,\\ 其中，M^{(l)}和b^{(l)}分别是第i层的权重矩阵和偏置向量.\\ f_r(h,t)=t^Tz^{(L)}.$$

将经过前向传播后的输出与t进行匹配得到score function。

---

神经网络图示

---

---

Semantic Matching Models的对比

---

Model Training

KG嵌入模型的训练可以遵循两种假设，open world assumption（开放世界假设）和closed world assumption（封闭世界假设）。

Open World Assumption（OWA）

OWA假设KGs中只包含正确的事实，不正确的事实是错误的或不存在的。$D^+$中只存有positive的例子，negative的例子由启发式模型生成（例如local closed world assumption），存放在$D^-$中。可以通过以下公式学习

$$\min_\Theta \sum_{\tau\in D^+\cup D^-}\log (1+\exp(-y_{hrt})\cdot f_r(h,t))),\\其中，\tau=(h,r,t)是训练样本，y_{hrt}= \pm1是标签（pos或neg）\\最小化logistic loss$$

除此之外，也可以使用pairwise ranking loss（可以使得pos facts评分比neg facts高）

$$\min_\Theta \sum_{\tau^+\in D^+}\sum_{\tau^- \in D^-}\max(0,\gamma-f_r(h,t)+f_{r^\prime}(h^\prime,t^\prime))\\其中，\tau^+是pos样本，\tau^-是neg样本，\gamma是其分界面.$$

使用pairwise ranking还有个优点，它不需要假设neg样本一定是错误的，因为本身这些neg样本就比pos样本更没有价值。

**logistic loss更适合semantic matching models（例如DistMult，ComplEx）而pairwise ranking更适合于translational distance models（例如TransE）

Open World Assumption训练过程

1. 初始化pos样本（通过平均分布或高斯分布，或者根据预训练的语料库）

2. 循环

   1. 从pos样本中去除少量样本集合p

   2. 对每个p中的pos样本生成对应的neg样本，并且加入到对应的集合

   $$D^-=\left\{(h^\prime,r,t)|h^\prime\in E \wedge h^\prime\neq h\wedge(h,r,t)\in D^+\right\}\\\cup \left\{(h,r,t^\prime)|t^\prime\in E\wedge t^\prime\neq t \wedge(h,r,t)\in D^+\right\}\\对head和tail随机选取$$

   或者关系也可以随机获取

   $$D^-=\left\{(h^\prime,r,t)|h^\prime\in E \wedge h^\prime\neq h\wedge(h,r,t)\in D^+\right\}\\\cup \left\{(h,r,t^\prime)|t^\prime\in E\wedge t^\prime\neq t \wedge(h,r,t)\in D^+\right\}\\\cup\left\{(h,r^\prime,t)|r^\prime\in R\wedge r^\prime\neq r \wedge(h,r,t)\in D^+\right\}$$

   注意到也有可能有这样的关系pos:(张三，性别，男)，生成了neg:(李四，性别，男)，显然这个neg是正确的，为了减少这种情况的发生，如果1-to-N，那么加大head被替换的概率，如果N-to-1，那么增大tail被替换的概率。

   1. 通过梯度下降更新每个实体和关系

3. 输出embeddings

值得注意的是，neg数量的提高可以带来更好的训练结果，50:1往往是个好的选择

Closed World Assumption（CWA）

CWA假设所有的不在$D^+$中的事实都是错误的，可以通过以下公式学习

$$\min_\Theta\sum_{h,t\in E,r\in R}(y_{hrt}-f_r(h,t))^2\\y_{hrt}=1((h,r,t)\in D^+);y_{hrt}=0(otherwise)$$

采取squard loss sums使得观测到事实接近1，未观测到的为0。

CWA有几个缺陷，

1. 对于不完整的KGs（缺失真实数据）效果较差。
2. 采用了大量的neg样本，可能导致模型的泛化能力较差。

Model Comparison

模型对比

使用外部信息

上述的各类模型方法仅使用了KG中的事实这一个角度来做embeddings。实际上，有很多外加的信息可以用来改善模型，比如实体类型（entity type），关系路径（relation paths），文本摘要（textual descriptions），逻辑规则（logical rules）等。

Entity Types

利用实体的类型信息，这些信息按理也存放在KG中，即IsA三元组。

Semantically smooth embedding（SSE）

SSE要求属于同一个类型的实体彼此之间应该很接近，它采用了两种流体学习的算法（manifold learning），Laplacian eigenmaps（拉普拉斯特征映射）和locally linear embedding（局部线性嵌入）

Laplacian eigenmaps

$$R_1=\frac{1}{2}\sum_{i=1}^n\sum_{j=1}^n\left\|e_i-e_j\right\|_2^2w_{ij}^1\\其中，e_i和e_j是实体嵌入的向量;\\w_{ij}^1=1\ if 两个实体属于同一个类\ w_{ij}^1=0$$

通过最小化R₁，期望同一个类下的实体距离会较小。

locally linear embedding

$$R_2=\sum_{i=1}^n\left\|e_i-\sum_{e_j\in \mathbb N_{e_i}}w_{ij}^2e_j\right\|_2^2,\\其中，\mathbb N_{e_i}是包含了每个实体e_i最近邻居;\\w_{ij}^2=1\ ife_j\in \mathbb N_{e_i} else \ w_{ij}^2=0$$

通过最小化R₂，期望每个实体能从其最近的邻居那里线性重建，并且具有较小误差

SSE的一个问题是它的类别是没有分层的，而且每个实体只能归于一个类

Type-embodied knowledge representation learing（TKRL）

TKRL被设计用来解决SSE中类型层次和多分类标签的问题

$$f_r(h,t)=-\left\|M_{rh}h+r-M_{rt}t\right\|_1,\\M_{rh}和M_{rt}是h,t的投影矩阵,\\为了解决多标签问题，M_{rh}是所有可能分类矩阵的权重之和\\ M_{rh}=\frac{\sum \nolimits_{i=1}^{n_h}a_iM_{c_i}}{\sum\nolimits_{i=1}^{n_h}a_i}$$